
【题目】如图①,A、B、C三地依次在一直线上,两辆汽车甲、乙分别从A、B两地同时出发驶向C地,如图②,是两辆汽车行驶过程中到C地的距离s(km)与行驶时间t(h)的关系图象,其中折线段EF﹣FG是甲车的图象,线段OM是乙车的图象.
(1)图②中,a的值为 ;点M的坐标为 ;
(2)当甲车在乙车与B地的中点位置时,求行驶的时间t的值.
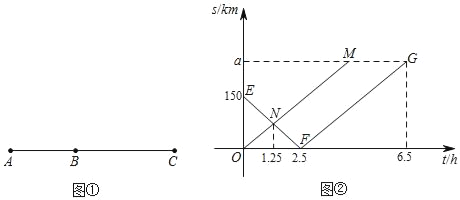
【答案】(1)240,(4,240);(2)t的值为2(h).
【解析】
(1)先求出直线EF的解析式,进而求出点N的坐标,再根据点N的坐标求出直线OM的解析式,进而求出直线FG的解析式,即可得出a的值;
(2)根据乙车行驶的路程与行驶时间的关系求解即可.
(1)设EF的解析式为y=k1x+150,
因为直线EF经过(2.5,0),所以2.5k1+150=0,解得k1=﹣60,
所以EF的解析式为y=﹣60x+150;
因为点M在EF上,所以点N的纵坐标为:﹣60×1.25+150=75,
因为点N的坐标为(1.25,75);
设直线OM的解析式为y=k2x,因为直线OM经过点N,所以1.25k2=75,解得k2=60,
所以直线OM的解析式为y=60x,
所以直线FG的解析式为y=60x﹣150,
所以点G的纵坐标,即a=60×6.5﹣150=240,
所以点M的横坐标为240÷60=4,即点M的坐标为(4,240).
故答案为:240;(4,240);
(2)由点M的坐标可知乙车的速度为240÷4=60(千米/时)
当甲车在乙车与B地的中点位置时,行驶的时间t的值为![]() =2(h).
=2(h).


科目:初中数学 来源: 题型:
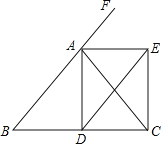
【题目】如图,已知△ABC中,AB=AC,AD是角平分线,F为BA延长线上的一点,AE平分∠FAC,DE∥BA交AE于E.求证:四边形ADCE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,AB=13,BC=12,点D,E分别是AB,BC的中点,连接DE,CD,如果DE=2.5,那么△ACD的周长是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=mx2+(2﹣2m)x+m﹣2(m是常数).
(1)无论m取何值,该抛物线都经过定点 D.直接写出点D的坐标.
(2)当m取不同的值时,该抛物线的顶点均在某个函数的图象上,求出这个函数的表达式.
(3)若在0≤x≤1的范围内,至少存在一个x的值,使y>0,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,∠ACB=90°,OC=2BO,AC=6,点B的坐标为(1,0),抛物线y=﹣x2+bx+c经过A、B两点.
(1)求点A的坐标;
(2)求抛物线的解析式;
(3)点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE=![]() DE.
DE.
①求点P的坐标;
②在直线PD上是否存在点M,使△ABM为直角三角形?若存在,求出符合条件的所有点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
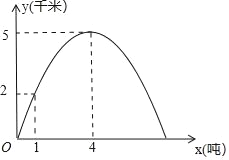
【题目】根据对宁波市相关的市场物价调研,某批发市场内甲种水果的销售利润y1(千元)与进货量x(吨)近似满足函数关系y1=0.25x,乙种水果的销售利润y2(千元)与进货量x(吨)之间的函数y2=ax2+bx+c的图象如图所示.
(1)求出y2与x之间的函数关系式;
(2)如果该市场准备进甲、乙两种水果共8吨,设乙水果的进货量为t吨,写出这两种水果所获得的销售利润之和W(千元)与t(吨)之间的函数关系式,并求出这两种水果各进多少吨时获得的销售利润之和最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
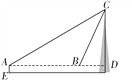
【题目】衡阳市城市标志来雁塔坐落在衡阳市雁峰公园内.如图,为了测量来雁塔的高度,在E处用高为1.5 m的测角仪AE,测得塔顶C的仰角为30°,再向塔身前进10.4 m,又测得塔顶C的仰角为60°,求来雁塔的高度.(结果精确到0.1 m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校运动会需购买A、B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元.
(1)求A、B两种奖品的单价各是多少元?
(2)学校计划购买A、B两种奖品共100件,且A种奖品的数量不大于B种奖品数量的3倍,设购买A种奖品m件,购买费用为W元,写出W(元)与m(件)之间的函数关系式.请您确定当购买A种奖品多少件时,费用W的值最少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com