
【题目】已知抛物线y=mx2+(2﹣2m)x+m﹣2(m是常数).
(1)无论m取何值,该抛物线都经过定点 D.直接写出点D的坐标.
(2)当m取不同的值时,该抛物线的顶点均在某个函数的图象上,求出这个函数的表达式.
(3)若在0≤x≤1的范围内,至少存在一个x的值,使y>0,求m的取值范围.
【答案】(1) 定点D(1,0);(2)在;(3)m>2.
【解析】
①当x=1时,y=0.说明无论m取何值,函数图像都经过同一个点(1,0),可求定点.
②根据抛物线方程求出顶点坐标,进而求出函数表达式.
③根据一二问求出抛物线与x轴的交点,再讨论对称轴与交点坐标的位置关系.
解:(1)∵抛物线y=mx2+(2﹣2m)x+m﹣2=m(x﹣1)2+2(x﹣1)
∴当x﹣1=0时,无论m为何值,抛物线经过定点 D,
∴x=1,y=0,
∴定点D(1,0);
(2)∵﹣![]() =﹣
=﹣![]() =1﹣
=1﹣![]() ,
,
![]() =
=![]() =﹣
=﹣![]() ,
,
∴顶点为(1﹣![]() ,﹣
,﹣![]() ),
),
∴顶点在函数y=x﹣1上;
(3)由(1)、(2)可得,该抛物线与x轴的一个交点为(1,0),对称轴为直线x=1﹣![]() .
.
①

当m>0时,抛物线开口方向向上,且1﹣![]() <1,
<1,
由图象可知,要满足条件,只要x=0式,y=m﹣2>0,
∴m>2;
②
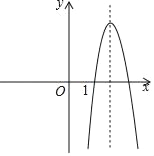
当m<0时,抛物线开口方向向下,且1﹣![]() >1,
>1,
由图象可知,不符合题意;
综上所述,m的取值范围是:m>2.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
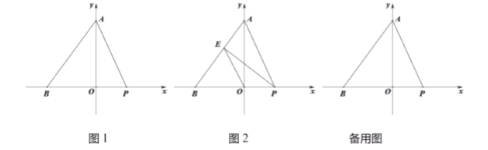
【题目】如图,已知A(3,0),B(0,-1),连接AB,过B点作AB的垂线段,使BA=BC,连接AC.
(1)如图1,求C点坐标;
(2)如图2,若P点从A点出发,沿x轴向左平移,连接BP,作等腰直角三角形△BPQ,连接CQ.求证:PA=CQ.
(3)在(2)的条件下,若C、P、Q三点共线,求此时P点坐标及∠APB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,垂足为点
,垂足为点![]() ,且
,且![]() ,连接
,连接![]() .
.
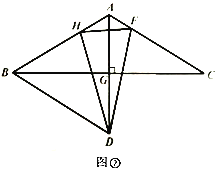
(1)如图①,求证:![]() 是等边三角形;
是等边三角形;

(2)如图①,若点![]() 、
、![]() 分别为
分别为![]() ,
,![]() 上的点,且
上的点,且![]() ,求证:
,求证:![]() ;
;
(3)利用(1)(2)中的结论,思考并解答:如图②,![]() 为
为![]() 上一点,连结
上一点,连结![]() ,当
,当![]() 时,线段
时,线段![]() ,
,![]() ,
,![]() 之间有何数量关系,给出证明.
之间有何数量关系,给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划销售甲、乙两种产品共![]() 件,每销售
件,每销售![]() 件甲产品可获得利润
件甲产品可获得利润![]() 万元, 每销售
万元, 每销售![]() 件乙产品可获得利润
件乙产品可获得利润![]() 万元,设该商场销售了甲产品
万元,设该商场销售了甲产品![]() (件),销售甲、乙两种产品获得的总利润为
(件),销售甲、乙两种产品获得的总利润为![]() (万元).
(万元).
(1)求![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)若每件甲产品成本为![]() 万元,每件乙产品成本为
万元,每件乙产品成本为![]() 万元,受商场资金影响,该商场能提供的进货资金至多为
万元,受商场资金影响,该商场能提供的进货资金至多为![]() 万元,求出该商场销售甲、乙两种产品各为多少件时,能获得最大利润.
万元,求出该商场销售甲、乙两种产品各为多少件时,能获得最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 坐标为
坐标为![]() ,点
,点![]() 是
是![]() 轴正半轴上一点,且
轴正半轴上一点,且![]() ,点
,点![]() 是
是![]() 轴上位于点
轴上位于点![]() 右侧的一个动点,设点
右侧的一个动点,设点![]() 的坐标为
的坐标为![]() .
.
(1)点![]() 的坐标为___________;
的坐标为___________;
(2)当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 点的坐标;
点的坐标;
(3)如图2,过点![]() 作
作![]() 交线段
交线段![]() 于点
于点![]() ,连接
,连接![]() ,若点
,若点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,当点
,当点![]() 恰好落在直线
恰好落在直线![]() 上时,
上时,![]() _____________.(直接写出答案)
_____________.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
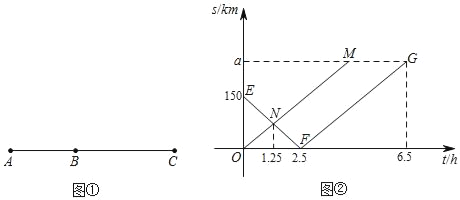
【题目】如图①,A、B、C三地依次在一直线上,两辆汽车甲、乙分别从A、B两地同时出发驶向C地,如图②,是两辆汽车行驶过程中到C地的距离s(km)与行驶时间t(h)的关系图象,其中折线段EF﹣FG是甲车的图象,线段OM是乙车的图象.
(1)图②中,a的值为 ;点M的坐标为 ;
(2)当甲车在乙车与B地的中点位置时,求行驶的时间t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是![]() 的的直径,BC
的的直径,BC![]() AB于点B,连接OC交
AB于点B,连接OC交![]() 于点E,弦AD//OC,弦DF
于点E,弦AD//OC,弦DF![]() AB于点G.
AB于点G.
(1)求证:点E是![]() 的中点;
的中点;
(2)求证:CD是![]() 的切线;
的切线;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com