
����Ŀ��ij�̳��ƻ����ۼס������ֲ�Ʒ��![]() ��,ÿ����
��,ÿ����![]() ���ײ�Ʒ�ɻ������
���ײ�Ʒ�ɻ������![]() ��Ԫ, ÿ����
��Ԫ, ÿ����![]() ���Ҳ�Ʒ�ɻ������
���Ҳ�Ʒ�ɻ������![]() ��Ԫ,����̳������˼ײ�Ʒ
��Ԫ,����̳������˼ײ�Ʒ![]() (��),���ۼס������ֲ�Ʒ��õ�������Ϊ
(��),���ۼס������ֲ�Ʒ��õ�������Ϊ![]() (��Ԫ).
(��Ԫ).
(1)��![]() ��
��![]() ֮��ĺ�������ʽ;
֮��ĺ�������ʽ;
(2)��ÿ���ײ�Ʒ�ɱ�Ϊ![]() ��Ԫ,ÿ���Ҳ�Ʒ�ɱ�Ϊ
��Ԫ,ÿ���Ҳ�Ʒ�ɱ�Ϊ![]() ��Ԫ,���̳��ʽ�Ӱ��,���̳����ṩ�Ľ����ʽ�����Ϊ
��Ԫ,���̳��ʽ�Ӱ��,���̳����ṩ�Ľ����ʽ�����Ϊ![]() ��Ԫ,������̳����ۼס������ֲ�Ʒ��Ϊ���ټ�ʱ,�ܻ���������.
��Ԫ,������̳����ۼס������ֲ�Ʒ��Ϊ���ټ�ʱ,�ܻ���������.
���𰸡�(1) y=-0.1x+100 (2) ���̳����ۼ�50������150��ʱ,�ܻ���������.
��������
(1) �������⼴���г�һ�κ��������ɣ�
(2) ��ļ���Ϊx����ô�ҵļ���Ϊ��200-x�����������г�����ʽ0.6x+0.8(200-x)��150�����������y=-0.1x+100�����ʣ��������.
�⣺(1)������ɵã�y=0.4x+0.5����200-x��
�õ���y=-0.1x+100
����y��x֮��ĺ�������ʽΪy=-0.1x+100
(2)��ļ���Ϊx����ô�ҵļ���Ϊ��200-x��
������ɵã�0.6x+0.8(200-x)��150
��ã�x��50
��y=-0.1x+100
�õ�y��x���������С
���Ե��������ʱ��xֵԽС����Խ��
���Լײ�Ʒx=50 �Ҳ�Ʒ200-x=150
�𣺸��̳����ۼ�50������150��ʱ,�ܻ���������.


 ��У��������ĩ��̾�ϵ�д�
��У��������ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������y=��x2��6x+21����
��1��ֱ��д��������y=��x2��6x+21�Ķ������ꣻ
��2����x��2ʱ����y��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�D��E�ֱ���BC��AC�е㣬BFƽ�֡�ABC����DE�ڵ�F��AB��8��BC��6����EF�ij�Ϊ(����)
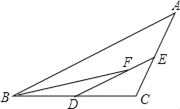
A. 1B. 2C. 3D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=13��BC=12����D��E�ֱ���AB��BC���е㣬����DE��CD�����DE=2.5����ô��ACD���ܳ���_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ι��ţ���������ˮ��2mʱ��ˮ���4m����ˮ���½�1mʱ��ˮ���������_____m��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=mx2+��2��2m��x+m��2��m�dz�������
��1������mȡ��ֵ���������߶��������� D��ֱ��д����D�����꣮
��2����mȡ��ͬ��ֵʱ���������ߵĶ������ij��������ͼ���ϣ������������ı���ʽ��
��3������0��x��1�ķ�Χ�ڣ����ٴ���һ��x��ֵ��ʹy��0����m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ACB��90����OC��2BO��AC��6����B������Ϊ��1��0����������y����x2+bx+c����A��B���㣮
��1�����A�����ꣻ
��2���������ߵĽ���ʽ��
��3����P��ֱ��AB�Ϸ��������ϵ�һ�㣬����P��PD��ֱx���ڵ�D�����߶�AB�ڵ�E��ʹPE��![]() DE��
DE��
�����P�����ꣻ
����ֱ��PD���Ƿ���ڵ�M��ʹ��ABMΪֱ�������Σ������ڣ�����������������е�M�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABCD�У���E��CD�ӳ�����һ�㣬BE��AD�ڵ�F��DE=![]() CD��
CD��
��1����֤����ABF�ס�CEB
��2������DEF�����Ϊ2����ABCD�������
��3����G��H�ֱ�ΪBF��AB���е㣬AG��FH���ڵ�O����![]() ��
��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com