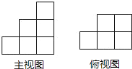
【题目】如图，组成这个几何体的小正方体的块数为
，则的所有可能值为________．
【答案】8，9，10，11
【解析】
由俯视图可得该组合几何体有3列，2行，以及最底层正方体的个数及摆放形状，由主视图结合俯视图可得从左边数第二列第二层最少有1个正方体，最多有2个正方体，第3列第2层，最少有1个正方体，最多有2个正方体，第3层最少有1个正方体，最多有2个正方体，分别相加得到组成组合几何体的最少个数及最多个数即可得到n的可能的值．
俯视图有5个正方形，
则最底层有5个正方体，
由主视图可得第2层最少有2个正方体，第3层最少有1个正方体；
由主视图可得第2层最多有4个正方体，第3层最多有2个正方体；
故n的值可能为：1+4+3=8，1+5+3=9，1+6+3=10，1+4+4=9，1+5+4=10，1+6+4=11，
故答案为：8，9，10，11．
计算高手系列答案科目：初中数学 来源： 题型：
【题目】在2018年韶关市开展的“善美韶关情暖三江”的志愿者系列括动中，某志愿者组织筹集了部分资金，计划购买甲、乙两种书包若干个送给贫困山区的学生，已知每个甲种书包的价格比每个乙种书包的价格贵10元，用350元购买甲种书包的个数恰好与用300元购买乙种书包的个数相同，求甲、乙两种书包每个的价格各是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点P是反比例函数
上第一象限上一个动点，点A、点B为坐标轴上的点，A（0，k），B（k，0）．已知△OAB的面积为
．
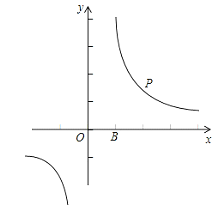
（1）求k的值；
（2）连接PA、PB、AB，设△PAB的面积为S，点P的横坐标为t．请直接写出S与t的函数关系式；
（3）阅读下面的材料回答问题：
当a＞0时，
∵
≥0，∴
≥2，即
≥2
由此可知：当
=0时，即a=1时，取得最小值2．
问题：请你根据上述材料探索（2）中△PAB的面积S有没有最小值？若有，请直接写出S的最小值；若没有，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点N(0，6)，点M在x轴负半轴上，ON＝3OM.A为线段MN上一点，AB⊥x轴，垂足为点B，AC⊥y轴，垂足为点C.
(1)写出点M的坐标；
(2)求直线MN的表达式；
(3)若点A的横坐标为－1，求矩形ABOC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
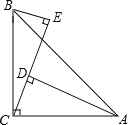
【题目】如图，∠ACB=90°，AC=BC，AD⊥CE，BE⊥CE，垂足分别为D，E．
（1）证明：△BCE≌△CAD；
（2）若AD=15cm，BE=8cm，求DE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,已知A(3，0),B(0，-1)，连接AB,过B点作AB的垂线段,使BA=BC,连接AC.
(1)如图1，求C点坐标；
(2)如图2,若P点从A点出发,沿x轴向左平移,连接BP,作等腰直角三角形△BPQ,连接CQ.求证:PA=CQ.
(3)在(2)的条件下,若C、P、Q三点共线,求此时P点坐标及∠APB的度数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图(十九)，用四个螺丝将四条不可弯曲的木条围成一个木框，不计螺丝大小，其中相邻两螺丝的距离依序为2、3、4、6，且相邻两木条的夹角均可调整。若调整木条的夹角时不破坏此木框，则任两螺丝的距离之最大值为何？
(A) 5 (B) 6 (C) 7 (D) 10
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商场计划销售甲、乙两种产品共
件,每销售
件甲产品可获得利润
万元, 每销售件乙产品可获得利润
万元,设该商场销售了甲产品
(件),销售甲、乙两种产品获得的总利润为
(万元).
(1)求与之间的函数表达式;
(2)若每件甲产品成本为
万元,每件乙产品成本为
万元,受商场资金影响,该商场能提供的进货资金至多为
万元,求出该商场销售甲、乙两种产品各为多少件时,能获得最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
