
已知二次函数 .
.
1.(1)求它的对称轴与 轴交点D的坐标;
轴交点D的坐标;
2.(2)将该抛物线沿它的对称轴向上平移,如图所示,设平移后的抛物线的顶点为 ,与
,与 轴、
轴、 轴的交点分别为A、B、C三点,连结AC、BC,若∠ACB=90°.
轴的交点分别为A、B、C三点,连结AC、BC,若∠ACB=90°.
①求此时抛物线的解析式;
②以AB为直径作圆,试判断直线CM与此圆的位置关系,并说明理由.

1..解:(1)由
得 
∴D(3,0) …………………………1分
2.(2)∵ 

∴顶点坐标
设抛物线向上平移h个单位,则得到 ,顶点坐标
,顶点坐标
∴平移后的抛物线:
 ……………………2分
……………………2分
当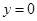 时,
时,
 ,
,
得 

∴ A B
B ……………………3分
……………………3分
易证△AOC∽△COB

∴ OA·OB
……………………4分
OA·OB
……………………4分

∴  ,
,
∴平移后的抛物线:
 ………5分
………5分
如图2, 由抛物线的解析式 可得
可得
 A(-2 ,0),B(8 ,0) C(0,4)
,
A(-2 ,0),B(8 ,0) C(0,4)
, ……………………6分
……………………6分
过C、M作直线,连结CD,过M作MH垂直y轴于H,[来源:]
则
∴

在Rt△COD中,CD= =AD
=AD
∴点C在⊙D上 ……………………7分
∴
∴
∴△CDM是直角三角形,
∴CD⊥CM
∴直线CM与⊙D相切
【解析】略


科目:初中数学 来源: 题型:
| A、y1≥y2 | B、y1>y2 | C、y1<y2 | D、y1≤y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•莒南县二模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
(2013•莒南县二模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:查看答案和解析>>
科目:初中数学 来源: 题型:
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①ac>0;②a-b+c<0;
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①ac>0;②a-b+c<0;查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com