
 如图,下列四组条件中:①AB=DE,BC=EF,AC=DF;②AB=DE,∠B=∠E,BC=EF;③AB=DE,AC=DF,∠B=∠E;④∠B=∠E,BC=EF,∠C=∠F.其中不一定能使△ABC≌△DEF的条件是③(只填序号).
如图,下列四组条件中:①AB=DE,BC=EF,AC=DF;②AB=DE,∠B=∠E,BC=EF;③AB=DE,AC=DF,∠B=∠E;④∠B=∠E,BC=EF,∠C=∠F.其中不一定能使△ABC≌△DEF的条件是③(只填序号). 分析 根据全等三角形的判定方法逐个判断即可.
解答 解:
①由AB=DE,BC=EF,AC=DF,可知在△ABC和△DEF中,满足SSS,可使△ABC≌△DEF;
②由AB=DE,∠B=∠E,BC=EF,可知在△ABC和△DEF中,满足SAS,可使△ABC≌△DEF;
③由AB=DE,AC=DF,∠B=∠E,可知在△ABC和△DEF中,满足SSA,不能使△ABC≌△DEF;
④由∠B=∠E,BC=EF,∠C=∠F,可知在△ABC和△DEF中,满足ASA,可使△ABC≌△DEF.
∴不一定能使△ABC≌△DEF的条件是③.
故答案为:③.
点评 本题主要考查全等三角形的判定,掌握全等三角形的判定方法是解题的关键,即SSS、SAS、ASA、AAS和HL.


科目:初中数学 来源: 题型:选择题
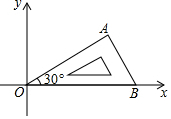 将含有30°角的直角三角板OAB如图放置在平面直角坐标中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为( )
将含有30°角的直角三角板OAB如图放置在平面直角坐标中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为( )| A. | ($\sqrt{3}$,1) | B. | (1,-$\sqrt{3}$) | C. | ($\sqrt{2}$,-$\sqrt{2}$) | D. | (-$\sqrt{2}$,$\sqrt{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,是直立在高速公路边水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为( )
如图,是直立在高速公路边水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为( )| A. | 4$\sqrt{3}$米 | B. | (2$\sqrt{3}$+2)米 | C. | (4$\sqrt{2}$-4)米 | D. | (4$\sqrt{3}$-4)米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
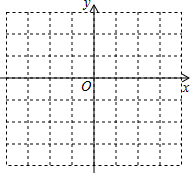 如图,△ABC的三个顶点在边长为1的正方形网格中,已知A(-1,-1),B(4,-1),C(3,1).
如图,△ABC的三个顶点在边长为1的正方形网格中,已知A(-1,-1),B(4,-1),C(3,1).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
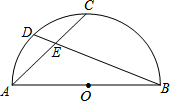 如图,AB是半圆O的直径,点C是$\widehat{AB}$的中点,点D是$\widehat{AC}$的中点,连接AC、BD交于点E,则$\frac{DE}{BE}$=$\frac{\sqrt{2}-1}{2}$.
如图,AB是半圆O的直径,点C是$\widehat{AB}$的中点,点D是$\widehat{AC}$的中点,连接AC、BD交于点E,则$\frac{DE}{BE}$=$\frac{\sqrt{2}-1}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com