
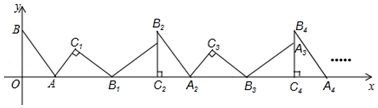
分析 根据图形和旋转规律可得出Bn点坐标的变换规律,结合三角形的周长,即可得出结论.
解答 解:在直角三角形OAB中,OA=$\frac{5}{3}$,OB=4,
由勾股定理可得:AB=$\frac{13}{3}$,
△OAB的周长为:OA+OB+AB=$\frac{5}{3}$+4+$\frac{13}{3}$=10,
研究三角形旋转可知,当n为偶数时Bn在最高点,当n为奇数时Bn在x轴上,横坐标规律为:
$\left\{\begin{array}{l}{\frac{n-1}{2}×10+6,(n为奇数)}\\{\frac{n}{2}×10,(n为偶数)}\end{array}\right.$,
∵2016为偶数,
∴B2016($\frac{2016}{2}$×10,4).
故答案为:(10080,4).
点评 本题考查的坐标与图形的变换,解题的关键是在变换中找到规律,结合图形得出结论.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:选择题
| A. | a-x=a-y | B. | x-y=0 | C. | ax=ay | D. | $\frac{x}{a+1}$=$\frac{y}{a+1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,下列四组条件中:①AB=DE,BC=EF,AC=DF;②AB=DE,∠B=∠E,BC=EF;③AB=DE,AC=DF,∠B=∠E;④∠B=∠E,BC=EF,∠C=∠F.其中不一定能使△ABC≌△DEF的条件是③(只填序号).
如图,下列四组条件中:①AB=DE,BC=EF,AC=DF;②AB=DE,∠B=∠E,BC=EF;③AB=DE,AC=DF,∠B=∠E;④∠B=∠E,BC=EF,∠C=∠F.其中不一定能使△ABC≌△DEF的条件是③(只填序号).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 (1)圆内接正六边形的边心距为$2\sqrt{3}$,则这个正六边形的面积为24$\sqrt{3}$cm2.
(1)圆内接正六边形的边心距为$2\sqrt{3}$,则这个正六边形的面积为24$\sqrt{3}$cm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com