练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
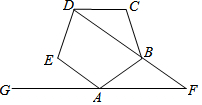
    16．如图，已知正五边形ABCDE，AF∥CD，交DB的延长线于点F，则∠DFA=36°．

    分析 首先求得正五边形内角∠C的度数，然后根据CD=CB求得∠CDB的度数，然后利用平行线的性质求得∠DFA的度数即可．

    解答 解：∵正五边形的外角为360°÷5=72°，
    ∴∠C=180°-72°=108°，
    ∵CD=CB，
    ∴∠CDB=36°，
    ∵AF∥CD，
    ∴∠DFA=∠CDB=36°．
    故答案为：36°．

    点评 本题考查了多边形的内角和外角及平行线的性质，解题的关键是求得正五边形的内角．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

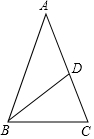    18．如图，等腰三角形ABC中，AB=AC，BD平分∠ABC，∠A=36°，则∠BDC的度数为（　　）
    A．36°B．60°C．108°D．72°

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．规定：a@b=2a-b 若：x@5=8，则 x=$\frac{13}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．若正多边形的一个内角是其外角的2倍，则这个多边形的边数是6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．在四个实数$\frac{3}{2}$，0，-1，$\sqrt{3}$中，最大的是$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

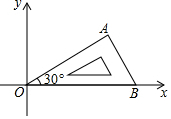    1．将含有30°角的直角三角板OAB如图放置在平面直角坐标中，OB在x轴上，若OA=2，将三角板绕原点O顺时针旋转75°，则点A的对应点A′的坐标为（　　）
    A．（$\sqrt{3}$，1）B．（1，-$\sqrt{3}$）C．（$\sqrt{2}$，-$\sqrt{2}$）D．（-$\sqrt{2}$，$\sqrt{2}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．如图，是直立在高速公路边水平地面上的交通警示牌，经测量得到如下数据：AM=4米，AB=8米，∠MAD=45°，∠MBC=30°，则警示牌的高CD为（　　）
    A．4$\sqrt{3}$米B．（2$\sqrt{3}$+2）米C．（4$\sqrt{2}$-4）米D．（4$\sqrt{3}$-4）米

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．如图，在平面直角坐标系中，将△ABO绕点A顺时针旋转到△AB1C1的位置，点B、O分别落在点B1、C1处，点B1在x轴上，再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置，点C2在x轴上，将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置，点A2在x轴上，依次进行下去…．若点A（$\frac{5}{3}$，0），B（0，4），则点B2016的横坐标为（10080，4）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．若抛物线的图象经过A（0，3），B（2，0），C（0，-2），D（5，3）中的三个点，则关于该抛物线的叙述正确的是（　　）
    A．不经过点AB．不经过点B
    C．开口向下D．顶点为（2.5，-0.125）

    查看答案和解析>>

    同步练习册答案