
| 1 |
| 10 |
| 1 |
| 10 |
| 1 |
| 10 |


科目:初中数学 来源: 题型:
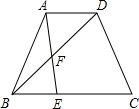 如图,等腰梯形ABCD中,AD∥BC,AD=1,BC=3,AB=CD=2,射线AB绕点A逆时针旋转分别与BD、BC交于点F、E,旋转角∠BAE=∠DBC,则BE=
如图,等腰梯形ABCD中,AD∥BC,AD=1,BC=3,AB=CD=2,射线AB绕点A逆时针旋转分别与BD、BC交于点F、E,旋转角∠BAE=∠DBC,则BE=查看答案和解析>>
科目:初中数学 来源: 题型:
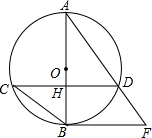 如图,AB为⊙O的直径,弦CD⊥AB于点H,过点B作⊙O的切线与AD的延长线交于F.
如图,AB为⊙O的直径,弦CD⊥AB于点H,过点B作⊙O的切线与AD的延长线交于F.| 3 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
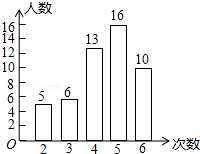 我市开展了“寻找雷锋足迹”的活动,某中学为了了解七年在“学雷锋活动月”中做好事的情况,随机调查了七年级50名学生在一个月内做好事的次数,并将所得数据绘制成统计图,请根据图中提供的信息解答下列问题:
我市开展了“寻找雷锋足迹”的活动,某中学为了了解七年在“学雷锋活动月”中做好事的情况,随机调查了七年级50名学生在一个月内做好事的次数,并将所得数据绘制成统计图,请根据图中提供的信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com