
【题目】如图,点A是反比例函数![]() 上的一个动点,连接OA,过点O作OB⊥OA,并且使OB=2OA,连接AB,当点A在反比函数图象上移动时,点B也在某一反比例函数图象
上的一个动点,连接OA,过点O作OB⊥OA,并且使OB=2OA,连接AB,当点A在反比函数图象上移动时,点B也在某一反比例函数图象![]() 上移动,
上移动, ![]() 的值为( )
的值为( )
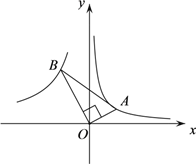
A. 2 B. -2 C. 4 D. -4
【答案】D
【解析】过A作AN⊥x轴于N,过B作BM⊥x轴于M. 设A(x, ![]() )(x>0),则ON×AN=1,由OB=2OA,通过△MBO∽△NOA的对应边成比例求得k=-OM×BM=-4.
)(x>0),则ON×AN=1,由OB=2OA,通过△MBO∽△NOA的对应边成比例求得k=-OM×BM=-4.
解:过A作AN⊥x轴于N,过B作BM⊥x轴于M.
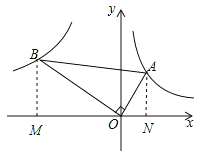
∵第一象限内的点A在反比例函数y的图象上,
∴设A(x, ![]() )(x>0),ON×AN=1,
)(x>0),ON×AN=1,
∵OB=2OA,t
∵OA⊥OB,
∴∠BMO=∠ANO=∠AOB=90°,
∴∠MBO+∠BOM=90°,∠MOB+∠AON=90°,
∴∠MB0=∠AON,
∴△MB0∽△NOA,∴![]() =
=![]() =
=![]() =2,
=2,
∴BM=2ON,OM=2AN,
又∵第二象限的点B在反比例函数y=![]() 上,
上,
∴k=-OM×BM=-2ON×2AN=-4.
故选D.
“点睛”本题考查了用待定系数法求出反比例函数的解析式,相似三角形的性质和判定的应用,解此题的关键是求出B的坐标.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】如图,P是矩形ABCD的对角线AC的中点,E是AD的中点.若AB=6,AD=8,则四边形ABPE的周长为( )
A.14
B.16
C.17
D.18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知□ABCD的对角线AC , BD相交于点O , 直线EF经过点O , 且分别交AB , CD于点E , F.求证:四边形BFDE是平行四边形..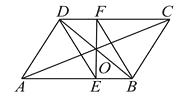

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.求证:四边形BCEF是平行四边形.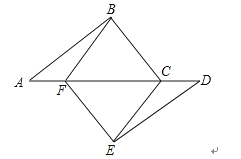
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于点F,连接CF。
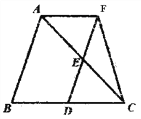
(1)求证:四边形ABDF是平行四边形;
(2)若∠CAF=45°,BC=4,CF=![]() ,求AB的长。
,求AB的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质,小静根据学习函数的经验,对函数
的图象与性质,小静根据学习函数的经验,对函数![]() 的图象与性质进行了探究,下面是小静的探究过程,请补充完整:
的图象与性质进行了探究,下面是小静的探究过程,请补充完整:
(1)函数![]() 的自变量x的取值范围是__________;
的自变量x的取值范围是__________;
(2)下表是y与x的几组对应值.
| … | -1 | 0 | 1 |
|
| 3 | 4 | … |
| … |
|
| 1 | 4 | m | 1 |
| … |
表中的m=__________;
p>(3)如图,在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,根据描出的点画出该函数的图象;
(4)结合函数图象,写出一条该函数图象的性质:______________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点Aa,b+0.5在x轴负半轴上,则点Bb21,a2在第______象限;在平面直角坐标系中,若点Pa,b在第二象限,则点Q1a,b在第______象限.
查看答案和解析>>
科目:初中数学 来源: 题型:
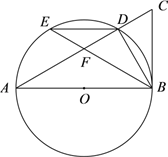
【题目】如图,AB为⊙O的直径,点D,E为⊙O上的两个点,延长AD至C,使∠CBD=∠BED.
(1)求证:BC是⊙O的切线;
(2)当点E为弧AD的中点且∠BED=30°时,⊙O半径为2,求DF的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com