
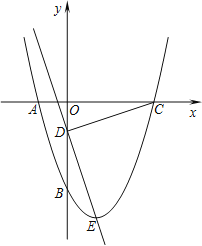
【题目】如图所示,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(﹣1,0)、(0,﹣3).
(1)求抛物线的函数解析式;
(2)点E为抛物线的顶点,点C为抛物线与x轴的另一交点,点D为y轴上一点,且DC=DE,求出点D的坐标;
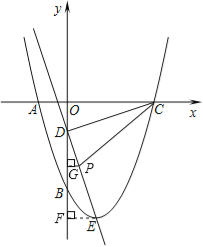
(3)在第二问的条件下,在直线DE上存在点P,使得以C、D、P为顶点的三角形与△DOC相似,请你直接写出所有满足条件的点P的坐标.
【答案】(1)y=x2﹣2x﹣3;(2)D(0,﹣1);(3)P点坐标(﹣![]() ,0)、(
,0)、(![]() ,﹣2)、(﹣3,8)、(3,﹣10).
,﹣2)、(﹣3,8)、(3,﹣10).
【解析】试题分析:(1)将A,B两点坐标代入解析式,求出b,c值,即可得到抛物线解析式;(2)先根据解析式求出C点坐标,及顶点E的坐标,设点D的坐标为(0,m),作EF⊥y轴于点F,利用勾股定理表示出DC,DE的长。再建立相等关系式求出m值,进而求出D点坐标;(3)先根据边角边证明△COD≌△DFE,得出∠CDE=90°,即CD⊥DE,然后当以C、D、P为顶点的三角形与△DOC相似时,根据对应边不同进行分类讨论:①当OC与CD是对应边时,有比例式![]() ,能求出DP的值,又因为DE=DC,所以过点P作PG⊥y轴于点G,利用平行线分线段成比例定理即可求出DG,PG的长度,根据点P在点D的左边和右边,得到符合条件的两个P点坐标;②当OC与DP是对应边时,有比例式
,能求出DP的值,又因为DE=DC,所以过点P作PG⊥y轴于点G,利用平行线分线段成比例定理即可求出DG,PG的长度,根据点P在点D的左边和右边,得到符合条件的两个P点坐标;②当OC与DP是对应边时,有比例式![]() ,易求出DP,仍过点P作PG⊥y轴于点G,利用比例式
,易求出DP,仍过点P作PG⊥y轴于点G,利用比例式![]() 求出DG,PG的长度,然后根据点P在点D的左边和右边,得到符合条件的两个P点坐标;这样,直线DE上根据对应边不同,点P所在位置不同,就得到了符合条件的4个P点坐标.
求出DG,PG的长度,然后根据点P在点D的左边和右边,得到符合条件的两个P点坐标;这样,直线DE上根据对应边不同,点P所在位置不同,就得到了符合条件的4个P点坐标.
试题解析:(1)∵抛物线y=x2+bx+c经过A(﹣1,0)、B(0,﹣3),∴![]() ,解得
,解得![]() ,故抛物线的函数解析式为y=x2﹣2x﹣3;(2)令x2﹣2x﹣3=0,解得x1=﹣1,x2=3,则点C的坐标为(3,0),∵y=x2﹣2x﹣3=(x﹣1)2﹣4,∴点E坐标为(1,﹣4),设点D的坐标为(0,m),作EF⊥y轴于点F(如下图),∵DC2=OD2+OC2=m2+32,DE2=DF2+EF2=(m+4)2+12,∵DC=DE,∴m2+9=m2+8m+16+1,解得m=﹣1,∴点D的坐标为(0,﹣1);(3)∵点C(3,0),D(0,﹣1),E(1,﹣4),∴CO=DF=3,DO=EF=1,根据勾股定理,CD=
,故抛物线的函数解析式为y=x2﹣2x﹣3;(2)令x2﹣2x﹣3=0,解得x1=﹣1,x2=3,则点C的坐标为(3,0),∵y=x2﹣2x﹣3=(x﹣1)2﹣4,∴点E坐标为(1,﹣4),设点D的坐标为(0,m),作EF⊥y轴于点F(如下图),∵DC2=OD2+OC2=m2+32,DE2=DF2+EF2=(m+4)2+12,∵DC=DE,∴m2+9=m2+8m+16+1,解得m=﹣1,∴点D的坐标为(0,﹣1);(3)∵点C(3,0),D(0,﹣1),E(1,﹣4),∴CO=DF=3,DO=EF=1,根据勾股定理,CD=![]() =
=![]() =
=![]() ,在△COD和△DFE中,∵
,在△COD和△DFE中,∵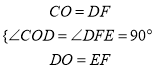 ,∴△COD≌△DFE(SAS),∴∠EDF=∠DCO,又∵∠DCO+∠CDO=90°,∴∠EDF+∠CDO=90°,∴∠CDE=180°﹣90°=90°,∴CD⊥DE,①当OC与CD是对应边时,∵△DOC∽△PDC,∴
,∴△COD≌△DFE(SAS),∴∠EDF=∠DCO,又∵∠DCO+∠CDO=90°,∴∠EDF+∠CDO=90°,∴∠CDE=180°﹣90°=90°,∴CD⊥DE,①当OC与CD是对应边时,∵△DOC∽△PDC,∴![]() ,即
,即![]() =
=![]() ,解得DP=
,解得DP=![]() ,过点P作PG⊥y轴于点G,则
,过点P作PG⊥y轴于点G,则![]() ,即
,即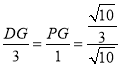 ,解得DG=1,PG=
,解得DG=1,PG=![]() ,当点P在点D的左边时,OG=DG﹣DO=1﹣1=0,所以点P(﹣
,当点P在点D的左边时,OG=DG﹣DO=1﹣1=0,所以点P(﹣![]() ,0),当点P在点D的右边时,OG=DO+DG=1+1=2,所以,点P(
,0),当点P在点D的右边时,OG=DO+DG=1+1=2,所以,点P(![]() ,﹣2);②当OC与DP是对应边时,∵△DOC∽△CDP,∴
,﹣2);②当OC与DP是对应边时,∵△DOC∽△CDP,∴![]() ,即
,即![]() =
=![]() ,解得DP=3
,解得DP=3![]() ,过点P作PG⊥y轴于点G,则
,过点P作PG⊥y轴于点G,则![]() ,即
,即![]() ,解得DG=9,PG=3,当点P在点D的左边时,OG=DG﹣OD=9﹣1=8,所以,点P的坐标是(﹣3,8),当点P在点D的右边时,OG=OD+DG=1+9=10,所以,点P的坐标是(3,﹣10),综上所述,在直线DE上存在点P,使得以C、D、P为顶点的三角形与△DOC相似,满足条件的点P共有4个,其坐标分别为(﹣
,解得DG=9,PG=3,当点P在点D的左边时,OG=DG﹣OD=9﹣1=8,所以,点P的坐标是(﹣3,8),当点P在点D的右边时,OG=OD+DG=1+9=10,所以,点P的坐标是(3,﹣10),综上所述,在直线DE上存在点P,使得以C、D、P为顶点的三角形与△DOC相似,满足条件的点P共有4个,其坐标分别为(﹣![]() ,0)、(
,0)、(![]() ,﹣2)、(﹣3,8)、(3,﹣10).
,﹣2)、(﹣3,8)、(3,﹣10).


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】成都市教育局和体育局都非常重视青少年球类运动的发展,经过多年的努力,全市青少年球类运动水平取得了大幅度提升.体育老师吴老师为了了解九年级学生喜欢球类运动的情况,抽取了该年级部分学生对篮球、足球、排球、乒乓球的爱好情况进行了调查,并将调查结果绘制成如下两幅不完整的统计图(说明:每位学生只选一种自己喜欢的一种球类),请根据这两幅图形解答下列问题:

(1)将两个不完整的统计图补充完整;
(2)九(1)班在本次调查中有3名女生和2名男生喜欢篮球,现从这5名学生中任意抽取2名学生当篮球队的队长,请用列表法或画树状图的方法求出刚好抽到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年10月12日至15日,第二届中国“互联网+”大学生创新创业全国总决赛上,ofo共享单车从全国约119000个创业项目中脱颖而出,最终获得金奖.将119000用科学记数法表示应为( )
A.1.19×104
B.0.119×106
C.1.19×105
D.11.9×104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是
①任何一个有理数的平方都是正数
②任何一个有理数的绝对值都是非负数
③如果一个有理数的倒数等于它本身,那么这个数是1
④如果一个有理数的相反数等于它本身,那么这个数是0
A. ①④ B. ②③ C. ③④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与x轴交于A,B两点,与y轴交于点C,连结AC、BC,D是线段OB上一动点,以CD为一边向右侧作正方形CDEF,连结BF,若S△OBC=8,AC=BC。
与x轴交于A,B两点,与y轴交于点C,连结AC、BC,D是线段OB上一动点,以CD为一边向右侧作正方形CDEF,连结BF,若S△OBC=8,AC=BC。
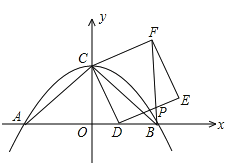
(1)求抛物线的解析式;
(2)求证:BF⊥AB;
(3)求∠FBE的度数;
(4)当D点沿x轴正方向移动到点B时,点E也随着移动,求点E所走过的路线长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着服装市场竞争日益激烈,某品牌服装专卖店一款服装按原售价降价a元后,再次降价20%,现售价为b元,设原售价为x元,列方程为
A. x-20%a=b B. (x-a)·20%=b
C. (x-a)·(1-20%)=b D. x-a-20%a=b
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com