
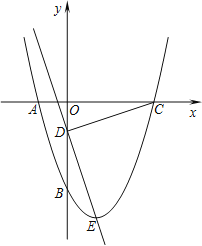
【题目】已知抛物线![]() 与x轴交于A,B两点,与y轴交于点C,连结AC、BC,D是线段OB上一动点,以CD为一边向右侧作正方形CDEF,连结BF,若S△OBC=8,AC=BC。
与x轴交于A,B两点,与y轴交于点C,连结AC、BC,D是线段OB上一动点,以CD为一边向右侧作正方形CDEF,连结BF,若S△OBC=8,AC=BC。
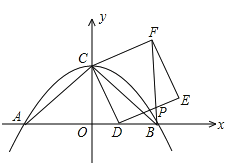
(1)求抛物线的解析式;
(2)求证:BF⊥AB;
(3)求∠FBE的度数;
(4)当D点沿x轴正方向移动到点B时,点E也随着移动,求点E所走过的路线长。
【答案】(1)抛物线的解析式为y=-![]() x2+4;(2)证明见解析;(3)45°;(4)4
x2+4;(2)证明见解析;(3)45°;(4)4![]() .
.
【解析】
试题分析:(1)根据抛物线的对称性得到抛物线的对称轴为y轴,则b=0;然后利用方程与二次函数的关系求得点B、C的坐标,由S△OBC=8可以求得c的值;
(2)由抛物线y=-![]() x2+4交x轴于点A、B,当x=0,求出图象与y轴的交点坐标,以及y=0,求出图象与x轴的交点坐标,即可得出三角形的形状;首先证明△ACD≌△BCF,利用三角形的全等,得出∠ABF=∠ABC+∠CBF=90°,即可得出答案;
x2+4交x轴于点A、B,当x=0,求出图象与y轴的交点坐标,以及y=0,求出图象与x轴的交点坐标,即可得出三角形的形状;首先证明△ACD≌△BCF,利用三角形的全等,得出∠ABF=∠ABC+∠CBF=90°,即可得出答案;
(3)如图,连接BE,过点E作EM⊥x轴于点M.易证△ODC≌△DME,则DM=OC=4,OD=EM.易求BM=EM.则∠MBE=∠MEB=45°;由(2)知,BF⊥AB,故
∠FBE=∠FBM-∠MBE=45°;
(4)由(3)知,点E在定直线上,当点D沿x轴正方向移动到点B时,点E所走过的路程长等于BC的长度.
试题解析:(1)如图,∵AC=BC,
∴该抛物线的对称轴是y轴,则b=0.
∴C(0,c),B(![]() ,0).
,0).
∵S△OBC=8,
∴![]() OCOB=
OCOB=![]() ×c×
×c×![]() =8,解得c=4(c>0).
=8,解得c=4(c>0).
故该抛物线的解析式为y=-![]() x2+4;
x2+4;
(2)证明:由(1)得到抛物线的解析式为y=-![]() x2+4;
x2+4;
令y=0,得x1=4,x2=-4,
∴A(-4,0),B(4,0),
∴OA=OB=OC,
∴△ABC是等腰直角三角形;
如图,又∵四边形CDEF是正方形,
∴AC=BC,CD=CF,∠ACD=∠BCF,
在△ACD和△BCF中
 ,
,
∴△ACD≌△BCF(SAS),
∴∠CBF=∠CAD=45°,
∴∠ABF=∠ABC+∠CBF=90°,
∴BF⊥AB;
(3)如图,连接BE,过点E作EM⊥x轴于点M.
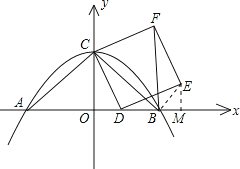
易证△ODC≌△DME,则DM=OC=4,OD=EM.
∵OD=OB-BD=4-BD=DM-BD=BM,
∴BM=EM.
∵∠EMB=90°,
由(2)知,BF⊥AB,
∴∠FBE=∠FBM-∠MBE=45°;
(4)由(3)知,点E在定直线上,当点D沿x轴正方向移动到点B时,点E所走过的路程长等于BC=4![]() .
.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣6,0),C(﹣1,0).
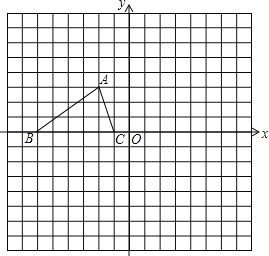
(1)请直接写出点B关于点A对称的点的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点B的对应点的坐标;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李明乘车回奶奶家,发现这条汽车线路上共有6个站(包括始发站和终点站),学习本节知识后,善于思考的小明已猜到这条线路上有多少种不同的票价,还要准备多少种不同的车票,聪明的你想到了吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(﹣1,0)、(0,﹣3).
(1)求抛物线的函数解析式;
(2)点E为抛物线的顶点,点C为抛物线与x轴的另一交点,点D为y轴上一点,且DC=DE,求出点D的坐标;
(3)在第二问的条件下,在直线DE上存在点P,使得以C、D、P为顶点的三角形与△DOC相似,请你直接写出所有满足条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,直线MN交⊙O于A、B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E。

(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①相反数等于它本身的数只有0;②倒数等于它本身的数有±1;③绝对值等于它本身的数是正数;④平方等于它本身的数只有1;其中错误的有:( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com