Question

在平面直角坐标xOy中，(如图)正方形OABC的边长为4，边OA在x轴的正半轴上，边OC在y轴的正半轴上，点D是OC的中点，BE⊥DB交x轴于点E．

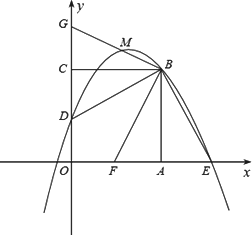
(1)求经过点D、B、E的抛物线的解析式；

(2)将∠DBE绕点B旋转一定的角度后，边BE交线段OA于点F，边BD交y轴于点G，交(1)中的抛物线于M(不与点B重合)，如果点M的横坐标为，那么结论OF＝DG能成立吗？请说明理由；

(3)过(2)中的点F的直线交射线CB于点P，交(1)中的抛物线在第一象限的部分于点Q，且使△PFE为等腰三角形，求Q点的坐标．

Answer 1

答案：
解析：

分析：(1)本题关键是求得E点坐标，然后利用待定系数法求抛物线解析式．如题图，可以证明△BCD≌△BAE，则AE＝CD，从而得到E点坐标； 　　(2)首先求出M点坐标，然后利用待定系数法求直线MB的解析式，令x＝0，求得G点坐标，进而得到线段CG、DG的长度；由△BCG≌△BAF，可得AF＝CG，从而求得OF的长度．比较OF与DG的长度，它们满足OF＝DG的关系，所以结论成立； 　　(3)本问关键在于分类讨论．△PFE为等腰三角形，如解答图所示，可能有三种情况，需逐一讨论并求解． 　　解答：解：(1)∵BE⊥DB交x轴于点E，OABC是正方形， 　　∴∠DBC＝EBA． 　　在△BCD与△BAE中， 　　∵， 　　∴△BCD≌△BAE，∴AE＝CD． 　　∵OABC是正方形，OA＝4，D是OC的中点， 　　∴A(4，0)，B(4，4)，C(0，4)，D(0，2)，∴E(6，0)． 　　设过点D(0，2)，B(4，4)，E(6，0)的抛物线解析式为y＝ax2＋bx＋c，则有： 　　， 　　解得， 　　∴经过点D、B、E的抛物线的解析式为：y＝－x2＋x＋2． 　　(2)结论OF＝DG能成立．理由如下： 　　由题意，当∠DBE绕点B旋转一定的角度后，同理可证得△BCG≌△BAF，∴AF＝CG． 　　∵xM＝，∴yM＝－xM2＋xM＋2＝，∴M(，)． 　　设直线MB的解析式为yMB＝kx＋b， 　　∵M(，)，B(4，4)， 　　∴， 　　解得， 　　∴yMB＝－x＋6， 　　∴G(0，6)， 　　∴CG＝2，DG＝4． 　　∴AF＝CG＝2，OF＝OA－AF＝2，F(2，0)． 　　∵OF＝2，DG＝4， 　　∴结论OF＝DG成立． 　　(3)如图，△PFE为等腰三角形，可能有三种情况，分类讨论如下： 　　①若PF＝FE． 　　∵FE＝4，BC与OA平行线之间距离为4， 　　∴此时P点位于射线CB上， 　　∵F(2，0)， 　　∴P(2，4)，此时直线FP⊥x轴， 　　∴xQ＝2， 　　∴yQ＝－xQ2＋xQ＋2＝，∴Q1(2，)； 　　②若PF＝PE． 　　如图所示，∵AF＝AE＝2，BA⊥FE， 　　∴△BEF为等腰三角形， 　　∴此时点P、Q与点B重合， 　　∴Q2(4，4)； 　　③若PE＝EF． 　　∵FE＝4，BC与OA平行线之间距离为4， 　　∴此时P点位于射线CB上， 　　∵E(6，0)，∴P(6，4)． 　　设直线yPF的解析式为yPF＝kx＋b，∵F(2，0)，P(6，4)， 　　∴， 　　解得， 　　∴yPF＝x－2． 　　∵Q点既在直线PF上，也在抛物线上， 　　∴－x2＋x＋2＝x－2，化简得5x2－14x－48＝0， 　　解得x1＝，x2＝－2(不合题意，舍去) 　　∴xQ＝2， 　　∴yQ＝xQ－2＝－2＝． 　　∴Q3(，)． 　　综上所述，Q点的坐标为Q1(2，)或Q2(4，4)或Q3(，)． 　　点评：本题是二次函数综合题，考查了二次函数的图象与性质、待定系数法求二次函数的解析式、待定系数法求一次函数解析式、解一元二次方程、全等三角形的判定与性质以及等腰三角形性质等知识点，考查内容涉及初中数学代数与几何的多个重要知识点，难度较大．本题第(3)问需要针对等腰三角形△PFE的三种可能情况进行分类讨论，避免漏解．

提示：

考点：二次函数综合题．