
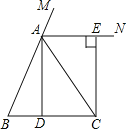
【题目】已知:如图,在△ABC中,AB=AC,点D为BC中点,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.求证:四边形ADCE为矩形.
【答案】证明见解析.
【解析】试题分析:根据AN是△ABC外角∠CAM的平分线,推得∠MAE=(∠B+∠ACB),再由∠B=∠ACB,得∠MAE=∠B,则AN∥BC,根据CE⊥AN,得出四边形ADCE为矩形.
证明:∵AN是△ABC外角∠CAM的平分线,
∴∠MAE=∠MAC,
∵∠MAC=∠B+∠ACB,
∵AB=AC,
∴∠B=∠ACB,
∴∠MAE=∠B,
∴AN∥BC,
∵AB=AC,点D为BC中点,
∴AD⊥BC,
∵CE⊥AN,
∴AD∥CE,
∴四边形ADCE为平行四边形(有两组对边分别平行的四边形是平行四边形),
∵CE⊥AN,
∴∠AEC=90°,
∴四边形ADCE为矩形(有一个角是直角的平行四边形是矩形).


科目:初中数学 来源: 题型:
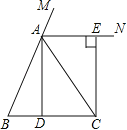
【题目】已知,点E、F分别在直线AB,CD上,点P在AB、CD之间,连结EP、FP,如图1,过FP上的点G作GH∥EP,交CD于点H,且∠1=∠2.
(1)求证:AB∥CD;
(2)如图2,将射线FC沿FP折叠,交PE于点J,若JK平分∠EJF,且JK∥AB,则∠BEP与∠EPF之间有何数量关系,并证明你的结论;
(3)如图3,将射线FC沿FP折叠,将射线EA沿EP折叠,折叠后的两射线交于点M,当EM⊥FM时,求∠EPF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标是(-1,2),作点A关于y轴对称得到点A′,再将点A′向上平移2个单位,得到点A′′,则点A′′的坐标是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位同学拿了两块45°三角尺△MNK,△ACB做了一个探究活动:将△MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=4.
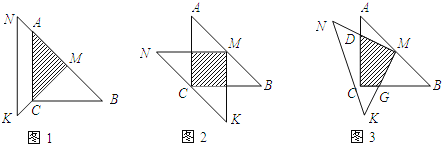
(1)如图1,两三角尺的重叠部分为△ACM,则重叠部分的面积为 ,周长为 .
(2)将图1中的△MNK绕顶点M逆时针旋转45°,得到图2,此时重叠部分的面积为 ,周长为 .
(3)如果将△MNK绕M旋转到不同于图1和图2的图形,如图3,请你猜想此时重叠部分的面积为 .
(4)在图3情况下,若AD=1,求出重叠部分图形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人出去散步,从家里出发,走了20min,到达一个离家900m的阅报亭,看了10min报纸后,用了15min返回家里,下面图象中正确表示此人离家的距离y(m)与时间x(min)之家关系的是( )
A.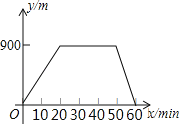 B.
B.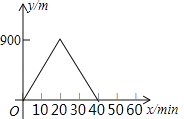
C.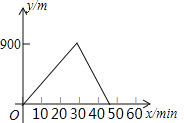 D.
D.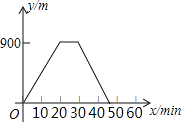
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若(x﹣2)(x+3)=x2+ax+b,则a,b的值分别为( )
A.a=5,b=﹣6
B.a=5,b=6
C.a=1,b=6
D.a=1,b=﹣6
查看答案和解析>>
科目:初中数学 来源: 题型:
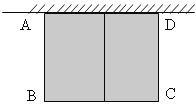
【题目】如图,有长为24米的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借用一段墙体(墙体的最大可用长度![]() 10米):如果AB的长为
10米):如果AB的长为![]() ,面积为
,面积为![]() .
.
(1)求面积![]() 与
与![]() 的函数关系(写出
的函数关系(写出![]() 的取值范围);
的取值范围);
(2)![]() 取何值时,面积最大?面积最大是多少?
取何值时,面积最大?面积最大是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com