练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】用一条长40cm的绳子围成一个面积为64cm2的矩形．设矩形的一边长为xcm，则可列方程为 ．

    【答案】x（20﹣x）=64．

    【解析】

    试题分析：设矩形的一边长为xcm，∵长方形的周长为40cm，∴宽为=（20﹣x）（cm），得x（20﹣x）=64．

    故答案为：x（20﹣x）=64．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】小明从今年1月初起刻苦练习跳远，每个月的跳远成绩都比上一个月有所增加，而且增加的距离相同．2月份，5月份他的跳远成绩分别为4.1m，4.7m．请你算出小明1月份的跳远成绩以及每个月增加的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD是正方形，△ADF旋转一定角度后得到△ABE，如果AF=4，AB=7．

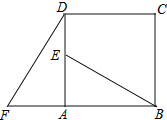
    （1）求BE的长；

    （2）在图中作出延长BE与DF的交点G，并说明BG⊥DF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，已知AB=AC，∠BAC=90°，BC=6cm，直线CM⊥BC，动点D从点C开始沿射线CB方向以每秒2厘米的速度运动，动点E也同时从点C开始在直线CM上以每秒1厘米的速度运动，连接AD、AE，设运动时间为t秒．

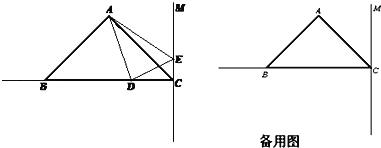
    （1）求AB的长；

    （2）当t为多少时，△ABD的面积为6cm2？

    （3）当t为多少时，△ABD≌△ACE，并简要说明理由．（可在备用图中画出具体图形）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知m，n是关于x的一元二次方程x2﹣3x+a=0的两个解，若（m﹣1）（n﹣1）=﹣6，则a的值为（ ）

    A．﹣10 B．4 C．﹣4 D．10

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在形如ab=N的式子中，我们已经研究两种情况：①已知a和b，求N，这是乘方运算，②已知b和N，求a，这是开放运算，现在我们研究第三种情况：已知a和N，求b，我们把这种运算叫做对数运算．

    定义：如果ab=N，（a＞0，a≠1，N＞0），则b叫做以a为底N的对数，记作：b=logaN，例如求log28，因为23=8，所以

    log8=3，又比如∵2﹣3=，∴log2=﹣3

    （1）根据定义计算：

    ①log381= ②log10=1③如果logx16=4，那么x=

    （2）设ax=M，ay=N，则logaM=x，logaN=y（a＞0，a≠1，M、N均为正数），

    ∵ax．ay=ax+y=M．N

    ∴logaMN=x+y，即logaMN=logaM+logaN

    这是对数运算的重要性质之一，进一步，我们还可以得出：

    logaM1M2M3…Mn= （其中M1、M2、M3…、Mn均为正数a＞0，a≠1）

    （3）请你猜想：loga= （a＞0，a≠1，M、N均为正数）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】兴发服装店老板用4500元购进一批某款T恤衫，由于深受顾客喜爱，很快售完，老板又用4950元购进第二批该款式T恤衫，所购数量与第一批相同，但每件进价比第一批多了9元．

    （1）第一批该款式T恤衫每件进价是多少元？

    （2）老板以每件120元的价格销售该款式T恤衫，当第二批T恤衫售出时，出现了滞销，于是决定降价促销，若要使第二批的销售利润不低于650元，剩余的T恤衫每件售价至少要多少元？（利润=售价﹣进价）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在东营市中小学标准化建设工程中，某学校计划购进一批电脑和电子白板，经过市场考察得知，购买1台电脑和2台电子白板需要3.5万元，购买2台电脑和1台电子白板需要2.5万元．

    （1）求每台电脑、每台电子白板各多少万元？

    （2）根据学校实际，需购进电脑和电子白板共30台，总费用不超过30万元，但不低于28万元，请你通过计算求出有几种购买方案，哪种方案费用最低．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在△ABC中，AB=AC，点D为BC中点，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E．求证：四边形ADCE为矩形．

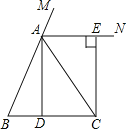
    查看答案和解析>>

    同步练习册答案