
【题目】在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
【答案】(1)每台电脑0.5万元,每台电子白板1.5万元;(2)方案3最省钱,即购买电脑17台,电子白板13台最省
【解析】
试题分析:(1)先设每台电脑x万元,每台电子白板y万元,根据购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元列出方程组,求出x,y的值即可;
(2)先设需购进电脑a台,则购进电子白板(30﹣a)台,根据需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元列出不等式组,求出a的取值范围,再根据a只能取整数,得出购买方案,再根据每台电脑的价格和每台电子白板的价格,算出总费用,再进行比较,即可得出最省钱的方案.
解:(1)设每台电脑x万元,每台电子白板y万元,根据题意得:
![]() ,
,
解得:![]() ,
,
答:每台电脑0.5万元,每台电子白板1.5万元;
(2)设需购进电脑a台,则购进电子白板(30﹣a)台,根据题意得:
![]() ,
,
解得:15≤a≤17,
∵a只能取整数,
∴a=15,16,17,
∴有三种购买方案,
方案1:需购进电脑15台,则购进电子白板15台,
方案2:需购进电脑16台,则购进电子白板14台,
方案3:需购进电脑17台,则购进电子白板13台,
方案1:15×0.5+1.5×15=30(万元),
方案2:16×0.5+1.5×14=29(万元),
方案3:17×0.5+1.5×13=28(万元),
∵28<29<30,
∴选择方案3最省钱,即购买电脑17台,电子白板13台最省钱.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:初中数学 来源: 题型:
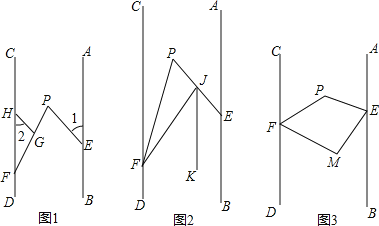
【题目】已知,点E、F分别在直线AB,CD上,点P在AB、CD之间,连结EP、FP,如图1,过FP上的点G作GH∥EP,交CD于点H,且∠1=∠2.
(1)求证:AB∥CD;
(2)如图2,将射线FC沿FP折叠,交PE于点J,若JK平分∠EJF,且JK∥AB,则∠BEP与∠EPF之间有何数量关系,并证明你的结论;
(3)如图3,将射线FC沿FP折叠,将射线EA沿EP折叠,折叠后的两射线交于点M,当EM⊥FM时,求∠EPF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标是(-1,2),作点A关于y轴对称得到点A′,再将点A′向上平移2个单位,得到点A′′,则点A′′的坐标是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若(x﹣2)(x+3)=x2+ax+b,则a,b的值分别为( )
A.a=5,b=﹣6
B.a=5,b=6
C.a=1,b=6
D.a=1,b=﹣6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com