
如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B、M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.
(1)判断AE与⊙O的位置关系,并说明理由;
(2)当BC=4,AC=3CE时,求⊙O的半径.

(1)相切,理由详见解析;(2)⊙O的半径为
【解析】
试题分析:(1)AE与⊙O相切,利用圆的性质和平行线的性质证明∠AMO=90°,即OM⊥AE即可;
(2)设⊙O的半径为r,则AO=6﹣r利用等腰三角形的性质和解直角三角形的有关知识以及利用平行线判定三角形相似和相似三角形的性质即可求出r的值.
试题解析:(1)AE与⊙O相切.
理由如下:
连接OM,则OM=OB,
∴∠OMB=∠OBM.
∵BM平分∠ABC,
∴∠OBM=∠EBM.
∴∠OMB=∠EBM.
∴OM∥BC.
∴∠AMO=∠AEB.
在△ABC中,AB=AC,AE是角平分线,
∴AE⊥BC.
∴∠AEB=90°.
∴∠AMO=90°.
∴OM⊥AE.
∴AE与⊙O相切;
(2)在△ABC中,AB=AC,AE是角平分线,
∴BE= BC,∠ABC=∠C.
BC,∠ABC=∠C.
∵BC=4,cosC= ,
,
∴BE=2,cos∠ABC= .
.
在△ABE中,∠AEB=90°,
∴ .
.
设⊙O的半径为r,则AO=6﹣r.
∵OM∥BC,
∴△AOM∽△ABE.
∴ .
.
∴ .
.
解得:r=
∴⊙O的半径为 .
.
考点:1. 切线的判定;2.相似三角形的判定与性质;3.解直角三角形.


科目:初中数学 来源:2013-2014学年浙江省宁波市九年级上学期期中考试数学试卷(解析版) 题型:填空题
点A(1,-2)为反比例函数y= 的图象上一点,则这个函数的解析式是 。
的图象上一点,则这个函数的解析式是 。
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省九年级直升班第一次综合测试数学试卷(解析版) 题型:解答题
如图,已知在△ABC中,AD是BC边上的中线,以AB为直径的⊙O交BC于点D,过D作MN⊥AC于点M,交AB的延长线于点N,过点B作BG⊥MN于G.

(1)求证:△BGD∽△DMA;
(2)求证:直线MN是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省中考模拟数学试卷(解析版) 题型:解答题
如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AE∥BC,DE∥AB.

证明:(1)AE=DC;
(2)四边形ADCE为矩形.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年新疆阿拉尔市九年级秋季班第一次月考数学试卷(解析版) 题型:解答题
已知一元二次方程kx2+(2k-1)x+k+2=0有两个不相等的实数根,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年广东省深圳市海怡翠学校九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,则PD的长为( )

A. B.
B.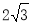 C.2 D.
C.2 D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com