
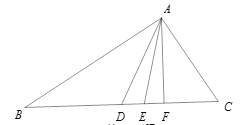
【题目】如图所示,三亚有三个车站A、B、C成三角形,一辆公共汽车从B站前往到C站。
(1)当汽车运动到点D时,刚好BD=CD,连接AD,AD这条线段是什么线段?这样的线段在△ABC中有几条?此时有面积相等的三角形吗?
(2)汽车继续向前运动,当运动到点E时,发现∠BAE=∠CAE,那么AE这条线段是什么线段?在△ABC中,这样的线段又有几条?
(3)汽车继续向前运动,当运动到点F时,发现∠AFB=∠AFC=90°,则AF是什么线段?在△ABC中,这样的线段有几条?
【答案】(1)AD是△ABC中BC边上的中线,三角形中有三条中线.此时△ABD与△ADC的面积相等。
(2)AE是△ABC中∠BAC的角平分线,三角形中角平分线有三条。
(3)AF是△ABC中BC边上的高线,三角形有三条高线。
【解析】(1)由于BD=CD,则点D是BC的中点,AD是中线,三角形的中线把三角形分成两个面积相等的三角形;(2)由于∠BAE=∠CAE,由AE是三角形的角平分线;(3)由于∠AFB=∠AFC=90°,则AF是三角形的高线.
解:(1)AD是△ABC中BC边上的中线,三角形中有三条中线.此时△ABD与△ADC的面积相等.
(2)AE是△ABC中∠BAC的角平分线,三角形上角平分线有三条.
(3)AF是△ABC中BC边上的高线,高线有时在三角形外部,三角形中有三条高线.
“点睛”本题考查了三角形的高线、角平分线、中线的概念,它们分别都有三条.


科目:初中数学 来源: 题型:
【题目】如图,由长度为1个单位的若干小正方形组成的网格图中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)三角形ABC的面积为
(3)以AC为边作与△ABC全等的三角形(只要作出一个符合条件的三角形即可);
(4)在直线l上找一点P,使PB+PC的长最短.

查看答案和解析>>
科目:初中数学 来源: 题型:
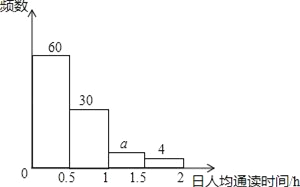
【题目】某校1200名学生参加了全区组织的“经典诵读”活动,该校随机选取部分学生,对他们在三、四两个月的诵读时间进行调查,下面是根据调查数据制作的统计图表的一部分.
根据以上信息,解答下列问题:
(1)本次调查的学生数为__人;
(2)图表中的a、b、c的值分别为__,__,__;
(3)在被调查的学生中,四月份日人均诵读时间在1<x≤1.5范围内的人数比三月份在此范围的人数多__人;
(4)试估计该校学生四月份人均诵读时间在1小时以上的人数.
四月日人均诵读时间的统计表
日人均诵读时间x/h | 人数 | 百分比 |
0≤x≤0.5 | 6 | |
0.5<x≤1 | 30 | |
1<x≤1.5 | 50% | |
1.5<x≤2 | 10 | 10% |
2<x≤2.5 | b | c |
三月日人均诵读时间的频数分布直方图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中![]() ,AO=BO,直线MN经过点O, 且AC⊥MN于C,BD⊥MN于D
,AO=BO,直线MN经过点O, 且AC⊥MN于C,BD⊥MN于D
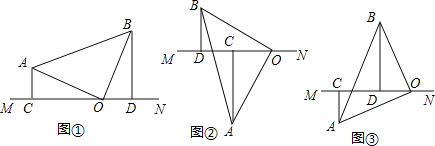
(1) 当直线MN绕点O旋转到图①的位置时,求证:CD=AC+BD;
(2) 当直线MN绕点O旋转到图②的位置时,求证:CD=AC-BD;
(3) 当直线MN绕点O旋转到图③的位置时,试问:CD、AC、BD有怎样的等量关系?请写出这个等量关系,并加以证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是若干名同学在引体向上训练时一次测试成绩(个)的频数分布折线图.

(1)参加这次测试共有多少名同学?
(2)组中点为9个一组的频数是多少?
(3)分布两端虚设的频数为零的是哪两组?
查看答案和解析>>
科目:初中数学 来源: 题型:
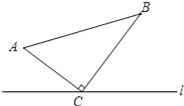
【题目】如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A→C→B路径向终点运动,终点为B点;点Q从B点出发沿B→C→A路径向终点运动,终点为A点.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.设运动时间为t秒,则当t=_________秒时,△PEC与△QFC全等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com