
【题目】(教材呈现)
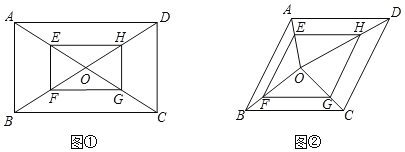
下图是华师版九年级上册数学教材第79页的部分内容.

请根据教材内容,结合图①,写出完整的解题过程.
(结论应用)
(1)在图①中,若AB=2,∠AOD=120°,则四边形EFGH的面积为______.
(2)如图②,在菱形ABCD中,∠BAD=120°,O是其内任意一点,连接O与菱形ABCD各顶点,四边形EFGH的顶点E、F、G、H分别在AO、BO、CO、DO上,EO=2AE,EF∥AB∥GH,且EF=GH,若△EFO与△GHO的面积和为![]() ,则菱形ABCD的周长为______.
,则菱形ABCD的周长为______.
【答案】![]() 24.
24.
【解析】
教材呈现:由矩形的性质得出OA=OB=OC=OD,再证出OE=OF=OG=OH,即可得出结论.
结论应用:(1)证明△OEF为等边三角形,得出∠EFO=60°,可求出EF=1,EH=![]() ,则答案可求出;
,则答案可求出;
(2)过点G作GN⊥EF于点N,由条件可知四边形EFGH为平行四边形,可得∠EFG=60°,设EF=x,则NG=![]() ,由△EFO与△GHO的面积和为4
,由△EFO与△GHO的面积和为4![]() 列出方程求出x,证明△OEF∽△OAB,可得
列出方程求出x,证明△OEF∽△OAB,可得![]() ,可求出AB的长.则答案可求出.
,可求出AB的长.则答案可求出.
解:教材呈现:
∵四边形ABCD是矩形,
∴OA=OC,OB=OD,AC=BD,
∴OA=OC=OB=OD.
∵AO,BO,CO,DO的中点E,F,G,H,
∴OE=OF=OG=OH,
∴四边形EFGH是矩形.
∵EG=FH,
∴四边形EFGH是矩形.
结论应用:
(1)∵AB=2,
∴EF=![]() .
.
∵∠BAD=90°,
∴∠FEH=90°.
∵∠AOD=120°,
∴∠EOF=60°,
∴△OEF为等边三角形,
∴∠EFO=60°,
∴![]() ,
,
∴四边形EFGH的面积为1×![]() .
.
故答案为:![]() .
.
(2)过点G作GN⊥EF于点N,
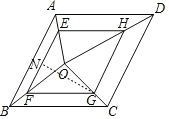
∵EF∥GH,且EF=GH,
∴四边形EFGH为平行四边形,
∴FG∥BC.
∵∠BAD=120°,
∴∠ABC=∠EFG=60°,
设EF=x,则NG=![]() .
.
∵△EFO与△GHO的面积和为4![]() ,
,
∴![]() ,
,
解得:x=4,∴EF=4.
∵EF∥AB,∴△OEF∽△OAB,
∴![]() .
.
∵EO=2AE,
∴![]() ,
,
∴AB=6,
∴菱形ABCD的周长为24.
故答案为:24.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
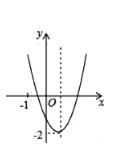
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c﹣m=0有两个不相等的实数根,下列结论:
①b2﹣4ac<0;②abc>0;③a﹣b+c<0;④m>﹣2,
其中,正确的个数有( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
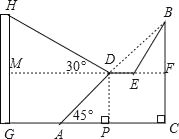
【题目】为邓小平诞辰110周年献礼,广安市政府对城市建设进行了整改,如图,已知斜坡AB长60![]() 米,坡角(即∠BAC)为45°,BC⊥AC,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE(下面两个小题结果都保留根号).
米,坡角(即∠BAC)为45°,BC⊥AC,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE(下面两个小题结果都保留根号).
(1)若修建的斜坡BE的坡比为![]() :1,求休闲平台DE的长是多少米?
:1,求休闲平台DE的长是多少米?
(2)一座建筑物GH距离A点33米远(即AG=33米),小亮在D点测得建筑物顶部H的仰角(即∠HDM)为30°.点B、C、A、G,H在同一个平面内,点C、A、G在同一条直线上,且HG⊥CG,问建筑物GH高为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
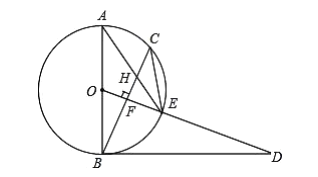
【题目】已知,如图,![]() 是⊙
是⊙![]() 的直径,点
的直径,点![]() 为⊙
为⊙![]() 上一点,
上一点,![]() 于点
于点![]() ,交⊙
,交⊙![]() 于点
于点![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() 为
为![]() 的延长线上一点,且
的延长线上一点,且![]() .
.
(1)试判断直线![]() 与⊙
与⊙![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若⊙![]() 的半径为
的半径为![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AB=10,AC=6.动点P从点A出发,沿折线AC﹣CB运动,在边AC上以每秒3个单位长度的速度运动,在边BC上以每秒4个单位长度的速度运动,到点B停止,当点P不与△ABC的顶点重合时,过点P作其所在直角边的垂线交AB于点Q;以Q为直角顶点向PQ右侧作Rt△PQD,且QD=![]() PQ.设△PQD与△ABC重叠部分图形的面积为S,点P运动的时间为t(s).
PQ.设△PQD与△ABC重叠部分图形的面积为S,点P运动的时间为t(s).
(1)当点P在边AC上时,求PQ的长(含t的代数式表示);
(2)点D落在边BC上时,求t的值;
(3)求S与t之间的函数关系式;
(4)设PD的中点为E,作直线CE.当直线CE将△PQD的面积分成1:5两部分时,直接写出t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
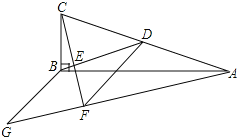
【题目】如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.
(1)求证:四边形BDFG为菱形;
(2)若AG=13,CF=6,求四边形BDFG的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将每件进价为20元的玩具以30元的价格出售时,每天可售出300件.经调查当单价每涨l元时,每天少售出10件.若商场想每天获得3750元利润,设每件玩具涨![]() 元,可列方程为:
元,可列方程为:![]()
![]()
![]() .对所列方程中出现的代数式,下列说法错误的是( )
.对所列方程中出现的代数式,下列说法错误的是( )
A.![]() 表示涨价后玩具的单价
表示涨价后玩具的单价
B.![]() 表示涨价后少售出玩具的数量
表示涨价后少售出玩具的数量
C.![]() 表示涨价后销售玩具的数量
表示涨价后销售玩具的数量
D.![]() 表示涨价后的每件玩具的单价
表示涨价后的每件玩具的单价
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店分两次购进![]() 、
、![]() 两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
购进数量(件) | 购进所需费用 (元) | ||
A | B | ||
第一次 | 20 | 50 | 4100 |
第二次 | 30 | 40 | 3700 |
(1)求![]() 、
、![]() 两种商品每件的进价分别是多少元?
两种商品每件的进价分别是多少元?
(2)商场决定![]() 商品以每件50元出售,
商品以每件50元出售,![]() 商品以每件
商品以每件![]() 元出售.为满足市场需求,需购进
元出售.为满足市场需求,需购进![]() 、
、![]() 两种商品共
两种商品共![]() 件,且
件,且![]() 商品的数量不少于
商品的数量不少于![]() 商品数量的
商品数量的![]() 倍,请你求出获利最大的进货方案,并确定最大利润.
倍,请你求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com