练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．已知，在△ABC中，AB=2，∠A=30°，BC=$\sqrt{2}$，则∠ABC=105°．

    分析 根据在△ABC中，AB=2，∠A=30°，BC=$\sqrt{2}$，由正弦定理可得∠C的值，从而可以求得本题的答案．

    解答 解：∵在△ABC中，AB=2，∠A=30°，BC=$\sqrt{2}$，
    ∴$\frac{BC}{sinA}=\frac{AB}{sinC}$
    即$\frac{\sqrt{2}}{\frac{1}{2}}=\frac{2}{sinC}$
    解得sinC=$\frac{\sqrt{2}}{2}$
    得∠C=45°
    ∴∠ABC=180°-∠A-∠C=180°-30°-45°=105°．
    故答案为：105°．

    点评 本题考查解直角三角形，关键是明确正弦定理的内容，找出求问题需要的条件．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    11．合并同类项
    （1）x3-2x2-x3-5+5x2+4；
    （2）2（a2b-3ab2）-3（2ab2-$\frac{5}{6}$a2b）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．已知：在△ABC中，∠BAC=120°．点P，Q在BC上，且△APQ是等边三角形．
    （1）求证：△ABP∽△CAQ；
    （2）若BP=3，CQ=2，求PQ的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．（1）若（m+1）x＜m+1的解集是x＞1，则化简$\sqrt{（m-1）^{2}}$得1-m，m-1
    （2）若关于x的方程x-3k+2=0的解是正数，则k的取值范围为k＜$\frac{2}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．若式子（2a-b）0+4a-2无意义，且2a+b=2，试求整式（2a-b）2-2（a-b）•（2a+b）+（2a+b）2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

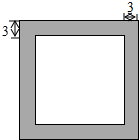    6．一标志性建筑的底面呈正方形，在其四周铺上花岗石，形成一个边宽为3米的正方形框（如图所示中阴影部分）已知铺这个框恰好用了192块边长为0.75米的正方形花岗石（接缝忽略不计），问标志性建筑底面的边长是多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

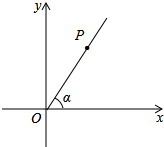    13．如图，点P是∠α的边OA上的一点，已知点P的横坐标为6，若sinα=$\frac{4}{5}$
    （1）求点P的纵坐标；
    （2）求∠α其它的三角函数值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．已知m、n、p为常数，若m+n+p=0，且m＞n＞p，在如下结论中：
    （1）m＞0，p＜0；
    （2）关于x的方程nx+m+p=0一定是一元一次方程；
    （3）m2016=（n+p）2016；
    （4）$\frac{|m|}{m}$+$\frac{|n|}{n}$+$\frac{|p|}{p}$+$\frac{|mp|}{mp}$ 的值为0或-2；
    （5）在数轴上点M、N、P表示数m、n、p，则OM=ON+OP或OP=ON+OM；
    （6）关于x的方程nx=3-mx-px有无数个解．
    正确结论的个数是（　　）
    A．2B．3C．4D．5

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

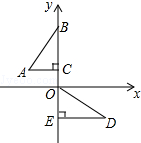    3．如图，在平面直角坐标系中，点B、C、E、在y轴上，Rt△ABC经过变换得到Rt△ODE．若点C的坐标为（0，2），AC=4，则这种变换可以是（　　）
    A．△ABC绕点C逆时针旋转90°，再向下平移2
    B．△ABC绕点C顺时针旋转90°，再向下平移2
    C．△ABC绕点C顺时针旋转90°，再向下平移6
    D．△ABC绕点C逆时针旋转90°，再向下平移6

    查看答案和解析>>

    同步练习册答案