
分析 (1)利用方程先求出x+$\frac{1}{x}$=3,把x2+$\frac{1}{{x}^{2}}$化为(x+$\frac{1}{x}$)2-2求解即可,
(2)把$\frac{{x}^{6}+3{x}^{3}+1}{2{x}^{3}}$化为$\frac{1}{2}$×[(x+$\frac{1}{x}$)(x2+$\frac{1}{{x}^{2}}$-1)+3求解即可
解答 解:∵x2-3x+1=0,
∴x-3+$\frac{1}{x}$=0,即x+$\frac{1}{x}$=3,
(1)x2+$\frac{1}{{x}^{2}}$=(x+$\frac{1}{x}$)2-2=7;
(2)$\frac{{x}^{6}+3{x}^{3}+1}{2{x}^{3}}$=$\frac{1}{2}$×(x3+3+$\frac{1}{{x}^{3}}$)=$\frac{1}{2}$×[(x+$\frac{1}{x}$)(x2+$\frac{1}{{x}^{2}}$-1)+3]=$\frac{1}{2}$×[3×6+3]=$\frac{21}{2}$.
点评 本题主要考查了分式的混合运算,解题的关键是正确求出x+$\frac{1}{x}$=3.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
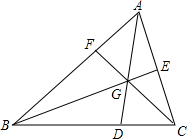 如图,在△ABC中,点D,E,F分别在三边上,E是AC的中点,AD,BE,CF交于一点G,BC=3DC,S△GEC=3,S△GBD=8,则△ABC的面积是30.
如图,在△ABC中,点D,E,F分别在三边上,E是AC的中点,AD,BE,CF交于一点G,BC=3DC,S△GEC=3,S△GBD=8,则△ABC的面积是30.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
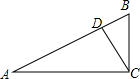 如图,在△ABC中,∠ACB=90°,D为AB边上一点,∠BCD=35°,∠BDC=80°.求∠A的度数.
如图,在△ABC中,∠ACB=90°,D为AB边上一点,∠BCD=35°,∠BDC=80°.求∠A的度数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com