
分析 ①对于直线解析式,令x=0表示出y,确定出A的坐标,过B作BF垂直于y轴,由直线与x轴夹角求出∠ABF度数,进而得到∠BAF为30°,在直角三角形ABF中,利用30度所对的直角边等于斜边的一半求出BF的长,即为B横坐标,代入直线解析式求出纵坐标,即可表示出B坐标;
②根据题意得到直线y=$\sqrt{3}$x+b向下平移b个单位,平移后解析式为y=$\sqrt{3}$x,此时M与O重合,由平移性质得到MN=AB=2,再由OC=2,且∠NMC=60°,得到三角形MNC为等边三角形,根据E为MC中点,利用三线合一得到NE垂直于MC,连接NE,交角平分线于点P,连接PC,此时PE+PC=PE+NP=NE最小,求出即可.
解答 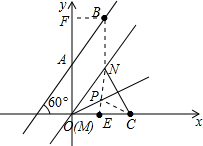 解:①对于直线y=$\sqrt{3}$x+b,
解:①对于直线y=$\sqrt{3}$x+b,
令x=0,得到y=b,即A(0,b),
过B作BF⊥y轴,交y轴于点F,
∵∠ABF=60°,
∴在Rt△ABF中,AB=2,∠BAF=30°,
∴BF=$\frac{1}{2}$AB=1,
把x=1代入y=$\sqrt{3}$x+b,得:y=$\sqrt{3}$+b,即B(1,$\sqrt{3}$+b);
②如图所示,由平移性质得:MN(ON)=AB=OC=2,且∠NMC=60°,直线MN解析式为y=$\sqrt{3}$x,
∴△MNC为等边三角形,
∵E为MC中点,
∴NE⊥MC,
∴在Rt△MNE中,MN=2,ME=1,
根据勾股定理得:NE=$\sqrt{3}$
连接NE,与角平分线OP交于点P,连接CP,此时PE+PC最小,且PE+PC=NE=$\sqrt{3}$.
点评 此题属于一次函数综合题,涉及的知识有:一次函数与坐标轴的交点,平移的性质,等边三角形的判定与性质,轴对称-线段最短问题,熟练掌握一次函数的性质是解本题的关键.


科目:初中数学 来源: 题型:填空题
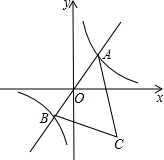 如图,已知A是双曲线y=$\frac{7}{x}$在第一象限的分支上一个动点,连接AO并延长另一分支于点B,以AB为一边作等边△ABC,点C在第四象限,随着点A的运动,点C的位置也不断发生变化,但点C始终在双曲线y=$\frac{k}{x}$(k<0)上运动,则k的值是-21.
如图,已知A是双曲线y=$\frac{7}{x}$在第一象限的分支上一个动点,连接AO并延长另一分支于点B,以AB为一边作等边△ABC,点C在第四象限,随着点A的运动,点C的位置也不断发生变化,但点C始终在双曲线y=$\frac{k}{x}$(k<0)上运动,则k的值是-21.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
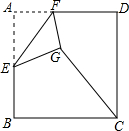 如图,在边长为2的正方形ABCD中,E是AB的中点,F是AD边上的一个动点,将△AEF沿EF所在直线折叠得到△GEF,连接GC,则GC长度的最小值是$\sqrt{5}$-1.
如图,在边长为2的正方形ABCD中,E是AB的中点,F是AD边上的一个动点,将△AEF沿EF所在直线折叠得到△GEF,连接GC,则GC长度的最小值是$\sqrt{5}$-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 尺规作图:(不写作法,保留作图痕迹)
尺规作图:(不写作法,保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
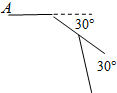 如图,王老师在上多边形外角和这节课时,做了一个活动,让小明在操场上从A点出发前进1m,向右转30°,再前进1m,又向右转30°,…,这样一直走下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形.小明一共走了12m,这个多边形的内角和是1800度.
如图,王老师在上多边形外角和这节课时,做了一个活动,让小明在操场上从A点出发前进1m,向右转30°,再前进1m,又向右转30°,…,这样一直走下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形.小明一共走了12m,这个多边形的内角和是1800度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com