
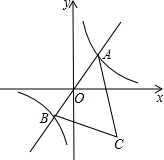
 如图,已知A是双曲线y=$\frac{7}{x}$在第一象限的分支上一个动点,连接AO并延长另一分支于点B,以AB为一边作等边△ABC,点C在第四象限,随着点A的运动,点C的位置也不断发生变化,但点C始终在双曲线y=$\frac{k}{x}$(k<0)上运动,则k的值是-21.
如图,已知A是双曲线y=$\frac{7}{x}$在第一象限的分支上一个动点,连接AO并延长另一分支于点B,以AB为一边作等边△ABC,点C在第四象限,随着点A的运动,点C的位置也不断发生变化,但点C始终在双曲线y=$\frac{k}{x}$(k<0)上运动,则k的值是-21. 分析 设点A的坐标为(x,$\frac{7}{x}$),连接OC,则OC⊥AB,表示出OC,过点C作CD⊥x轴于点D,设出点C坐标,在Rt△OCD中,利用勾股定理可得出x2的值,继而得出y与x的函数关系式.
解答 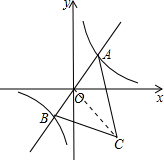 解:设A(x,$\frac{7}{x}$),
解:设A(x,$\frac{7}{x}$),
∵点A与点B关于原点对称,
∴OA=OB,
∵△ABC为等边三角形,
∴AB⊥OC,OC=$\sqrt{3}$AO,
∵AO=$\sqrt{{x}^{2}+(\frac{7}{x})^{2}}$,
∴CO=$\sqrt{3{x}^{2}+\frac{147}{{x}^{2}}}$,
过点C作CD⊥x轴于点D,
则可得∠AOD=∠OCD(都是∠COD的余角),
设点C的坐标为(a,b),则tan∠AOD=tan∠OCD,即$\frac{\frac{7}{x}}{x}$=$\frac{a}{-b}$,
解得:b=-$\frac{{x}^{2}}{7}$a,
在Rt△COD中,CD2+OD2=OC2,即b2+a2=3x2+$\frac{147}{{x}^{2}}$,
将b=-$\frac{{x}^{2}}{7}$a代入,可得:x2=$\frac{27}{{x}^{2}}$,
故x=$\frac{3\sqrt{3}}{3}$,b=-$\frac{{a}^{2}}{3}$,a=-$\sqrt{3}$x,
则ab=-21,
故可得:y=-$\frac{21}{x}$(x>0).
故答案是:-21.
点评 本题考查了反比例函数的综合题,涉及了解直角三角形、等边三角形的性质及勾股定理的知识,综合考察的知识点较多,解答本题的关键是将所学知识融会贯通,注意培养自己解答综合题的能力.


科目:初中数学 来源: 题型:填空题
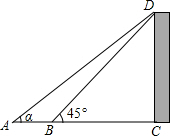 如图,在A处看建筑物CD的顶端D的仰角为α,且tanα=0.7,向前行进3米到达B处,从B处看D的仰角为45°(图中各点均在同一平面内,A、B、C三点在同一条直线上,CD⊥AC),则建筑物CD的高度为7米.
如图,在A处看建筑物CD的顶端D的仰角为α,且tanα=0.7,向前行进3米到达B处,从B处看D的仰角为45°(图中各点均在同一平面内,A、B、C三点在同一条直线上,CD⊥AC),则建筑物CD的高度为7米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
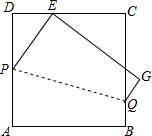 如图,把一块边长为6的正方形纸片ABCD沿着PQ翻折,使顶点A恰好与CD边上的点E重合,若DE=2,则折痕PQ=2$\sqrt{10}$.
如图,把一块边长为6的正方形纸片ABCD沿着PQ翻折,使顶点A恰好与CD边上的点E重合,若DE=2,则折痕PQ=2$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
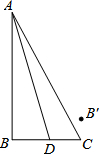 如图,已知∠B=90°,AB=3cm,BC=$\sqrt{3}$cm,点D是线段BC上的一个动点,连接AD,动点B′始终与点B关于直线AD对称,当点D由点B位置向右运动至点C位置时,相应的点B′所经过的路程为( )
如图,已知∠B=90°,AB=3cm,BC=$\sqrt{3}$cm,点D是线段BC上的一个动点,连接AD,动点B′始终与点B关于直线AD对称,当点D由点B位置向右运动至点C位置时,相应的点B′所经过的路程为( )| A. | 3cm | B. | πcm | C. | 2$\sqrt{3}$cm | D. | 2πcm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
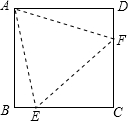 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,
如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com