
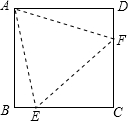
 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,
如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,分析 由正方形的性质得AB=AD,∠B=∠D=90°,由等边三角形的性质得AE=AF,则可判断Rt△ABE≌△ADF,得到BE=DF,∠BAE=∠DAF,加上∠EAF=60°,易得∠BAE=∠DAF=15°,利用互余得∠AEB=75°,则可对③进行判断;由于CB=CD,BE=DF,则CE=CF,于是可对②进行判断;先判断△CEF为等腰直角三角形得到CE=CF=$\frac{\sqrt{2}}{2}$EF=$\sqrt{2}$,设正方形的边长为x,则AB=x,BE=x-$\sqrt{2}$,在Rt△ABE中利用勾股定理得x2+(x-$\sqrt{2}$)2=22,解得x1=$\frac{\sqrt{2}+\sqrt{6}}{2}$,x2=$\frac{\sqrt{2}-\sqrt{6}}{2}$(舍去),则可计算出BE+DF=$\sqrt{6}$-$\sqrt{2}$,于是可判断①错误;然后利用正方形面积公式可对④进行判断.
解答 解:∵四边形ABCD为正方形,
∴AB=AD,∠B=∠D=90°,
∵△AEF为等边三角形,
∴AE=AF,
在Rt△ABE和△ADF中,
$\left\{\begin{array}{l}{AE=AF}\\{AB=AD}\end{array}\right.$,
∴Rt△ABE≌△ADF,
∴BE=DF,∠BAE=∠DAF,
而∠EAF=60°,
∴∠BAE=∠DAF=15°,
∴∠AEB=75°,所以③正确,
∵CB=CD,
∴CB-BE=CD-DF,
即CE=CF,所以②正确;
∴△CEF为等腰直角三角形,
∴CE=CF=$\frac{\sqrt{2}}{2}$EF=$\sqrt{2}$,
设正方形的边长为x,则AB=x,BE=x-$\sqrt{2}$,
在Rt△ABE中,∵AB2+BE2=AE2,
∴x2+(x-$\sqrt{2}$)2=22,
整理得x2-$\sqrt{2}$x-1=0,解得x1=$\frac{\sqrt{2}+\sqrt{6}}{2}$,x2=$\frac{\sqrt{2}-\sqrt{6}}{2}$(舍去),
∴BE+DF=2(x-$\sqrt{2}$)=2($\frac{\sqrt{2}+\sqrt{6}}{2}$-$\sqrt{2}$)=$\sqrt{6}$-$\sqrt{2}$≠2,所以①错误;
∴S正方形ABCD=x2=($\frac{\sqrt{2}+\sqrt{6}}{2}$)2=2+$\sqrt{3}$,所以④正确.
故答案为②③④.
点评 本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质.也考查了全等三角形的判定与性质和等边三角形的性质.


 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:解答题
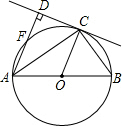 如图,AB为⊙O的直径,OC为⊙O的半径,AD⊥DC于D,AC平分∠DAB,AD交⊙O于点E.
如图,AB为⊙O的直径,OC为⊙O的半径,AD⊥DC于D,AC平分∠DAB,AD交⊙O于点E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
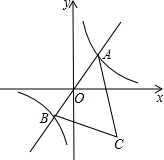 如图,已知A是双曲线y=$\frac{7}{x}$在第一象限的分支上一个动点,连接AO并延长另一分支于点B,以AB为一边作等边△ABC,点C在第四象限,随着点A的运动,点C的位置也不断发生变化,但点C始终在双曲线y=$\frac{k}{x}$(k<0)上运动,则k的值是-21.
如图,已知A是双曲线y=$\frac{7}{x}$在第一象限的分支上一个动点,连接AO并延长另一分支于点B,以AB为一边作等边△ABC,点C在第四象限,随着点A的运动,点C的位置也不断发生变化,但点C始终在双曲线y=$\frac{k}{x}$(k<0)上运动,则k的值是-21.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
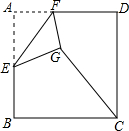 如图,在边长为2的正方形ABCD中,E是AB的中点,F是AD边上的一个动点,将△AEF沿EF所在直线折叠得到△GEF,连接GC,则GC长度的最小值是$\sqrt{5}$-1.
如图,在边长为2的正方形ABCD中,E是AB的中点,F是AD边上的一个动点,将△AEF沿EF所在直线折叠得到△GEF,连接GC,则GC长度的最小值是$\sqrt{5}$-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 尺规作图:(不写作法,保留作图痕迹)
尺规作图:(不写作法,保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com