
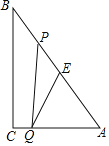
ЁОЬтФПЁПШчЭМЃЌRtЁїABCжаЃЌЁЯC=90ЁуЃЌBC=8cmЃЌAC=6cmЃЎЕуPДгBГіЗЂбиBA ЯђAдЫЖЏЃЌЫйЖШЮЊУПУы1cmЃЌЕуEЪЧЕуBвдPЮЊЖдГЦжааФЕФЖдГЦЕуЃЎЕуPдЫЖЏЕФЭЌЪБЃЌЕуQДгAГіЗЂбиACЯђCдЫЖЏЃЌЫйЖШЮЊУПУы2cm ЃЎЕБЕуQЕНДяЖЅЕуCЪБЃЌPЃЌQЭЌЪБЭЃжЙдЫЖЏЃЎЩшPЃЌ QСНЕудЫЖЏЪБМфЮЊtУыЃЎ
ЃЈ1ЃЉЕБtЮЊКЮжЕЪБЃЌPQЁЮBC ЃП
ЃЈ2ЃЉЩшЫФБпаЮPQCBЕФУцЛ§ЮЊyЃЌЧѓyЙигкtЕФКЏЪ§НтЮіЪН;
ЃЈ3ЃЉЫФБпаЮPQCBЕФУцЛ§гыЁїAPQУцЛ§БШФмЮЊ3ЃК2Т№ЃПШєФмЃЌЧѓГіДЫЪБtЕФжЕЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ4ЃЉЕБtЮЊКЮжЕЪБЃЌЁїAEQЮЊЕШбќШ§НЧаЮЃП
ЁОД№АИЁПЃЈ1ЃЉtЃН![]() ЃЛЃЈ2ЃЉyЃН
ЃЛЃЈ2ЃЉyЃН![]() t2Љ8t+24ЃЛЃЈ3ЃЉЫФБпаЮPQCBУцЛ§ФмЪЧЁїABCУцЛ§ЕФ
t2Љ8t+24ЃЛЃЈ3ЃЉЫФБпаЮPQCBУцЛ§ФмЪЧЁїABCУцЛ§ЕФ![]() ЃЌДЫЪБtЕФжЕЮЊ5Љ
ЃЌДЫЪБtЕФжЕЮЊ5Љ![]() ЃЛРэгЩМћНтЮіЃЛЃЈ4ЃЉЕБtЮЊ
ЃЛРэгЩМћНтЮіЃЛЃЈ4ЃЉЕБtЮЊ![]() Уы
Уы![]() Уы
Уы![]() УыЪБЃЌЁїAEQЮЊЕШбќШ§НЧаЮЃЎ
УыЪБЃЌЁїAEQЮЊЕШбќШ§НЧаЮЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЯШдк![]() жаЃЌгЩЙДЙЩЖЈРэЧѓГі
жаЃЌгЩЙДЙЩЖЈРэЧѓГі![]() ЃЌдйгЩ
ЃЌдйгЩ![]() ЃЌ
ЃЌ![]() ЃЌЕУГі
ЃЌЕУГі![]() ЃЌШЛКѓгЩ
ЃЌШЛКѓгЩ![]() ЃЌИљОнЦНааЯпЗжЯпЖЮГЩБШР§ЖЈРэЕУГі
ЃЌИљОнЦНааЯпЗжЯпЖЮГЩБШР§ЖЈРэЕУГі![]() ЃЌСаГіБШР§ЪН
ЃЌСаГіБШР§ЪН![]() ЃЌЧѓНтМДПЩЃЛ
ЃЌЧѓНтМДПЩЃЛ
ЃЈ2ЃЉИљОн![]() ЃЌМДПЩЕУГі
ЃЌМДПЩЕУГі![]() Йигк
Йигк![]() ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉИљОнЬтвтжЊЫФБпаЮ![]() УцЛ§ЪЧ
УцЛ§ЪЧ![]() УцЛ§ЕФ
УцЛ§ЕФ![]() ЃЌСаГіЗНГЬ
ЃЌСаГіЗНГЬ![]() ЃЌНтЗНГЬМДПЩЃЛ
ЃЌНтЗНГЬМДПЩЃЛ
ЃЈ4ЃЉ![]() ЮЊЕШбќШ§НЧаЮЪБЃЌЗжШ§жжЧщПіЬжТлЃКЂй
ЮЊЕШбќШ§НЧаЮЪБЃЌЗжШ§жжЧщПіЬжТлЃКЂй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂл
ЃЛЂл![]() ЃЌУПвЛжжЧщПіЖМПЩвдСаГіЙигк
ЃЌУПвЛжжЧщПіЖМПЩвдСаГіЙигк![]() ЕФЗНГЬЃЌНтЗНГЬМДПЩ.
ЕФЗНГЬЃЌНтЗНГЬМДПЩ.
ЃЈ1ЃЉRtЁїABCжаЃЌЁпЁЯCЃН90ЁуЃЌBCЃН8cmЃЌACЃН6cmЃЌ
ЁрABЃН10cmЃЎ
ЁпBPЃНtЃЌAQЃН2tЃЌ
ЁрAPЃНABЉBPЃН10ЉtЃЎ
ЁпPQЁЮBCЃЌ
Ёр![]()
Ёр![]()
НтЕУtЃН![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЁпSЫФБпаЮPQCBЃНSЁїACBЉSЁїAPQЃН![]() ACBCЉ
ACBCЉ![]() APAQsinA
APAQsinA
ЁрyЃН![]() ЁС6ЁС8Љ
ЁС6ЁС8Љ![]() ЁСЃЈ10ЉtЃЉ2t
ЁСЃЈ10ЉtЃЉ2t![]()
ЃН24Љ![]() tЃЈ10ЉtЃЉ
tЃЈ10ЉtЃЉ
ЃН![]() t2Љ8t+24ЃЌ
t2Љ8t+24ЃЌ
МДyЙигкtЕФКЏЪ§ЙиЯЕЪНЮЊyЃН![]() t2Љ8t+24ЃЛ
t2Љ8t+24ЃЛ
ЃЈ3ЃЉЫФБпаЮPQCBУцЛ§ФмЪЧЁїABCУцЛ§ЕФ![]() ЃЌРэгЩШчЯТЃК
ЃЌРэгЩШчЯТЃК
гЩЬтвтЃЌЕУ![]() t2Љ8t+24ЃН
t2Љ8t+24ЃН![]() ЁС24ЃЌ
ЁС24ЃЌ
ећРэЃЌЕУt2Љ10t+12ЃН0ЃЌ
НтЕУt1ЃН5Љ![]() ЃЌt2ЃН5+
ЃЌt2ЃН5+![]() ЃЈВЛКЯЬтвтЩсШЅЃЉЃЎ
ЃЈВЛКЯЬтвтЩсШЅЃЉЃЎ
ЙЪЫФБпаЮPQCBУцЛ§ФмЪЧЁїABCУцЛ§ЕФ![]() ЃЌДЫЪБtЕФжЕЮЊ5Љ
ЃЌДЫЪБtЕФжЕЮЊ5Љ![]() ЃЛ
ЃЛ
ЃЈ4ЃЉЁїAEQЮЊЕШбќШ§НЧаЮЪБЃЌЗжШ§жжЧщПіЬжТлЃК
ЂйШчЙћAEЃНAQЃЌФЧУД10Љ2tЃН2tЃЌНтЕУtЃН![]() ЃЛ
ЃЛ
ЂкШчЙћEAЃНEQЃЌФЧУДЃЈ10Љ2tЃЉЁС![]() ЃНtЃЌНтЕУtЃН
ЃНtЃЌНтЕУtЃН![]() ЃЛ
ЃЛ
ЂлШчЙћQAЃНQEЃЌФЧУД2tЁС![]() ЃН5ЉtЃЌНтЕУtЃН
ЃН5ЉtЃЌНтЕУtЃН![]() ЃЎ
ЃЎ
ЙЪtЮЊ![]() Уы
Уы![]() Уы
Уы![]() УыЪБЃЌЁїAEQЮЊЕШбќШ§НЧаЮЃЎ
УыЪБЃЌЁїAEQЮЊЕШбќШ§НЧаЮЃЎ


 УПШе10ЗжжгПкЫуаФЫуЫйЫуЬьЬьСЗЯЕСаД№АИ
УПШе10ЗжжгПкЫуаФЫуЫйЫуЬьЬьСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌBA=BC=20cmЃЌAC=30cmЃЌЕуPДгAЕуГіЗЂЃЌбизХABвдУПУы4cmЕФЫйЖШЯђBЕудЫЖЏЃЛЭЌЪБЕуQДгCЕуГіЗЂЃЌбизХCAвдУПУы3cmЕФЫйЖШЯђAЕудЫЖЏЃЌЩшдЫЖЏЪБМфЮЊxУыЃЎ
ЃЈ1ЃЉxЮЊКЮжЕЪБЃЌPQЁЮBCЃЛ
ЃЈ2ЃЉЪЧЗёДцдкФГвЛЪБПЬЃЌЪЙЁїAPQЁзЁїCQBЃПШєДцдкЃЌЧѓГіДЫЪБAPЕФГЄЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
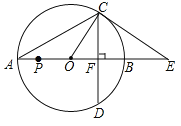
ЁОЬтФПЁПШчЭМЃЌвдABЮЊжБОЖЕФЁбOгыCEЯрЧагкЕуCЃЌCEНЛABЕФбгГЄЯпгкЕуEЃЌжБОЖABЃН18ЃЌЁЯAЃН30ЁуЃЌЯвCDЁЭABЃЌДЙзуЮЊЕуFЃЌСЌНгACЃЌOCЃЌдђЯТСаНсТле§ШЗЕФЪЧ______ЃЎЃЈаДГіЫљгае§ШЗНсТлЕФађКХЃЉ
Ђй![]() ЃЛ
ЃЛ
ЂкЩШаЮOBCЕФУцЛ§ЮЊ![]() ІаЃЛ
ІаЃЛ
ЂлЁїOCFЁзЁїOECЃЛ
ЂмШєЕуPЮЊЯпЖЮOAЩЯвЛЖЏЕуЃЌдђAPOPгазюДѓжЕ20.25ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЖўДЮКЏЪ§ yЃНax2+bx+cЃЈaЁй0ЃЉЕФЭМЯѓгы x жсНЛгкЕу AЃЈЉ1ЃЌ0ЃЉЃЌЖдГЦжсЮЊжБЯп xЃН1ЃЌгы y жсЕФНЛЕу B дкЃЈ0ЃЌ2ЃЉКЭЃЈ0ЃЌ3ЃЉжЎМфЃЈАќРЈетСНЕуЃЉЃЌЯТСаНсТле§ШЗЕФЪЧ_______________ЃЎ
ЂйЕБ xЃО3 ЪБЃЌyЃМ0ЃЛЂк3a+bЃМ0ЃЛЂлЉ1ЁмaЁмЉ![]() ЃЛЂм4acЉb2ЃМ8aЃЎ
ЃЛЂм4acЉb2ЃМ8aЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИЇЫГЪаФГаЃЯыжЊЕРбЇЩњЖдЁАвЃдЖЕФКеЭМАЂРЁБЃЌЁАЦьХлЙЪРяЁБЕШМвЯчТУгЮЦЗХЦЕФСЫНтГЬЖШЃЌЫцЛњГщШЁСЫВПЗжбЇЩњНјааЮЪОэЕїВщЃЌЮЪОэгаЫФИібЁЯюЃЈУПЮЛБЛЕїВщЕФбЇЩњБибЁЧвжЛбЁвЛЯюЃЉAЃЎЪЎЗжСЫНтЃЌBЃЎСЫНтНЯЖрЃЌCЃЎСЫНтНЯЩйЃЌDЃЎВЛжЊЕРЃЎНЋЕїВщЕФНсЙћЛцжЦГЩШчЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЌЧыИљОнСНЗљЭГМЦЭМжаЕФаХЯЂЛиД№ЯТСаЮЪЬтЃК
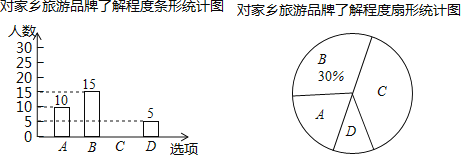
ЃЈ1ЃЉБОДЮЕїВщСЫЖрЩйУћбЇЩњЃП
ЃЈ2ЃЉВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉИУаЃЙВга500УћбЇЩњЃЌЧыФуЙРМЦЁАЪЎЗжСЫНтЁБЕФбЇЩњгаЖрЩйУћЃП
ЃЈ4ЃЉдкБЛЕїВщЁАЪЎЗжСЫНтЁБЕФбЇЩњжагаЫФУћбЇЩњЛсИЩВПЃЌЫћУЧжага3УћФаЩњКЭ1УћХЎЩњЃЌбЇаЃЯыДгет4ШЫжаШЮбЁСНШЫзіМвЯчТУгЮЦЗХЦаћДЋдБЃЌЧыгУСаБэЛђЛЪїзДЭМЗЈЧѓГіБЛбЁжаЕФСНШЫЧЁКУЪЧвЛФавЛХЎЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
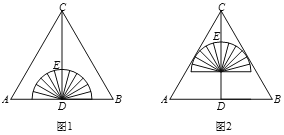
ЁОЬтФПЁПШчЭМ1ЃЌНЋвЛИіСПНЧЦїгывЛеХЕШБпШ§НЧаЮ(ЁїABC)жНЦЌЗХжУГЩжсЖдГЦЭМаЮЃЌCDЁЭAB,ДЙзуЮЊDЃЌАыдВ(СПНЧЦї)ЕФдВаФгыЕуDжиКЯЃЌДЫЪБЃЌВтЕУЖЅЕуCЕНСПНЧЦїзюИпЕуЕФОрРыCEЃН2cmЃЌНЋСПНЧЦїбиDCЗНЯђЦНвЦ1cmЃЌАыдВ(СПНЧЦї)ЧЁгыЁїABCЕФБпACЃЌBCЯрЧаЃЌШчЭМ2,дђABЕФГЄЮЊ__________cm.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЕу
жаЃЌЕу![]() ЃЌНЋЕуAЯђгвЦНвЦ6ИіЕЅЮЛГЄЖШЃЌЕУЕНЕуB.
ЃЌНЋЕуAЯђгвЦНвЦ6ИіЕЅЮЛГЄЖШЃЌЕУЕНЕуB.
(1)жБНгаДГіЕуBЕФзјБъЃЛ
(2)ШєХзЮяЯпy=-x2+bx+cОЙ§ЕуA,BЃЌЧѓХзЮяЯпЕФБэДяЪНЃЛ
(3)ШєХзЮяЯпy=-x2+bx+cЕФЖЅЕудкжБЯпy=x+2ЩЯвЦЖЏЃЌЕБХзЮяЯпгыЯпЖЮABгаЧвжЛгавЛИіЙЋЙВЕуЪБЃЌЧѓХзЮяЯпЖЅЕуКсзјБъ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
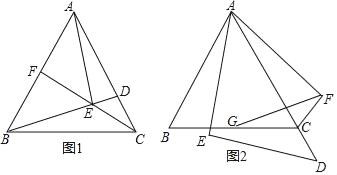
ЁОЬтФПЁПШчЭМЃЌдкЕШБпЁїABCжаЃЌЕуDЪЧACБпЩЯвЛЕуЃЌСЌНгBDЃЌЙ§ЕуAзїAEЁЭBDгкEЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌСЌНгCEВЂбгГЄCEНЛABгкЕуFЃЌШєЁЯCBDЃН15ЁуЃЌABЃН4ЃЌЧѓCEЕФГЄЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБЕуDдкЯпЖЮACЕФбгГЄЯпЩЯЪБЃЌНЋЯпЖЮAEШЦЕуAФцЪБеыа§зЊ60ЁуЕУЕНЯпЖЮAFЃЌСЌНгEFЃЌНЛBCгкGЃЌСЌНгCFЃЌЧѓжЄЃКBGЃНCGЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁРквЊжЦзївЛИіШ§НЧаЮЕФИжМмФЃаЭЃЌдкетИіШ§НЧаЮжаЃЌГЄЖШЮЊx(ЕЅЮЛЃКcm)ЕФБпгыетЬѕБпЩЯЕФИпжЎКЭЮЊ40 cmЃЌетИіШ§НЧаЮЕФУцЛ§S(ЕЅЮЛЃКcm2)Ыцx(ЕЅЮЛЃКcm)ЕФБфЛЏЖјБфЛЏЃЎ
ЃЈ1ЃЉЧыжБНгаДГіSгыxжЎМфЕФКЏЪ§ЙиЯЕЪН(ВЛвЊЧѓаДГіздБфСПxЕФШЁжЕЗЖЮЇ)ЃЛ
ЃЈ2ЃЉЕБxЪЧЖрЩйЪБЃЌетИіШ§НЧаЮУцЛ§SзюДѓ?зюДѓУцЛ§ЪЧЖрЩй?![]()
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com