
【题目】为了在即将到来的体育中考中取得好的成绩,某校准备在体育中考前将学校九年级的![]() 名学生送到体育馆进行一次模拟考试,经学校和客车公司联系了解到,
名学生送到体育馆进行一次模拟考试,经学校和客车公司联系了解到,![]() 辆大型客车和
辆大型客车和![]() 辆中型客车可载客
辆中型客车可载客![]() 人,
人,![]() 辆大型客车和
辆大型客车和![]() 辆中型客车可载客
辆中型客车可载客![]() 人,若要将这些学生--次性全部送到体育馆,且恰好装满.根据以上信息,回答下面问题:
人,若要将这些学生--次性全部送到体育馆,且恰好装满.根据以上信息,回答下面问题:
(1)每辆大型客车和中型客车各载多少人?
(2)该校共有多少种租车方案?.
(3)若每辆大型客车需租金![]() 元,每辆中型客车需租金
元,每辆中型客车需租金![]() 元,请你给该校提供一个最省钱的租车建议,并求出最少租车费用是多少?
元,请你给该校提供一个最省钱的租车建议,并求出最少租车费用是多少?
【答案】(1)每辆大型客车可载客![]() 人,每辆中型客车可载客
人,每辆中型客车可载客![]() 人(2)该校共有五种租车方案:①租用大型客车
人(2)该校共有五种租车方案:①租用大型客车![]() 辆,中型客车
辆,中型客车![]() 辆②租用大型客车
辆②租用大型客车![]() 辆,中型客车
辆,中型客车![]() 辆③租用大型客车
辆③租用大型客车![]() 辆,中型客车
辆,中型客车![]() 辆④租用大型客车
辆④租用大型客车![]() 辆,中型客车
辆,中型客车![]() 辆⑤租用大型客车
辆⑤租用大型客车![]() 辆,中型客车
辆,中型客车![]() 辆(3)建议该学校选择方案①租用大型客车
辆(3)建议该学校选择方案①租用大型客车![]() 辆,中型客车
辆,中型客车![]() 辆最省钱,最少的租车费用是
辆最省钱,最少的租车费用是![]() 元
元
【解析】
(1)设每辆大型客车可载客![]() 人,每辆中型客车可载客
人,每辆中型客车可载客![]() 人,根据“
人,根据“![]() 辆大型客车和
辆大型客车和![]() 辆中型客车可载客
辆中型客车可载客![]() 人,
人,![]() 辆大型客车和
辆大型客车和![]() 辆中型客车可载客
辆中型客车可载客![]() 人”列出二元一次方程组,解方程组即可得解;
人”列出二元一次方程组,解方程组即可得解;
(2)设租用大型客车![]() 辆,中型客车
辆,中型客车![]() 辆可将
辆可将![]() 名学生--次性全部送到体育馆,且恰好装满,可列出一个二元一次方程,解出该方程的非负整数解即可得到答案;
名学生--次性全部送到体育馆,且恰好装满,可列出一个二元一次方程,解出该方程的非负整数解即可得到答案;
(3)由(2)的结论,分别计算出五种方案的租车费用,然后比较大小,从中选择租车费用最少的即可得解.
解:(1)设每辆大型客车可载客![]() 人,每辆中型客车可载客
人,每辆中型客车可载客![]() 人,根据题意得,
人,根据题意得,
![]()
解得![]()
答:每辆大型客车可载客![]() 人,每辆中型客车可载客
人,每辆中型客车可载客![]() 人.
人.
(2)设租用大型客车![]() 辆,中型客车
辆,中型客车![]() 辆可将
辆可将![]() 名学生--次性全部送到体育馆,且恰好装满,根据题意得,
名学生--次性全部送到体育馆,且恰好装满,根据题意得,![]()
∴![]()
∵![]() 、
、![]() 均为非负整数
均为非负整数
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
答:该校共有五种租车方案:①租用大型客车![]() 辆,中型客车
辆,中型客车![]() 辆②租用大型客车
辆②租用大型客车![]() 辆,中型客车
辆,中型客车![]() 辆③租用大型客车
辆③租用大型客车![]() 辆,中型客车
辆,中型客车![]() 辆④租用大型客车
辆④租用大型客车![]() 辆,中型客车
辆,中型客车![]() 辆⑤租用大型客车
辆⑤租用大型客车![]() 辆,中型客车
辆,中型客车![]() 辆.
辆.
(3)①当租用大型客车![]() 辆、中型客车
辆、中型客车![]() 辆时,租车费用为
辆时,租车费用为![]() 元;
元;
②当租用大型客车![]() 辆、中型客车
辆、中型客车![]() 辆时,租车费用为
辆时,租车费用为![]() 元;
元;
③当租用大型客车![]() 辆、中型客车
辆、中型客车![]() 辆时,租车费用为
辆时,租车费用为![]() 元;
元;
④当租用大型客车![]() 辆、中型客车
辆、中型客车![]() 辆时,租车费用为
辆时,租车费用为![]() 元;
元;
⑤当租用大型客车![]() 辆、中型客车
辆、中型客车![]() 辆时,租车费用为
辆时,租车费用为![]() 元.
元.
∵![]()
∴建议该学校选择方案①租用大型客车![]() 辆,中型客车
辆,中型客车![]() 辆最省钱,最少的租车费用是
辆最省钱,最少的租车费用是![]() 元.
元.


科目:初中数学 来源: 题型:
【题目】某校举办“迎亚运”学生书画展览,现要在长方形展厅中划出3个形状、大小完全一样的小长方方形“图中阴影部分”区域摆放作品.
(1)如图1,若大长方形的长和宽分别为45米和30米,求小长方形的长和宽;
(2)如图2,若大长方形的长和宽分别为![]() 和
和![]() .
.
①直接写出1个小长方形周长与大长方形周长之比;
②若作品展览区域(阴影部分)面积占展厅面积的![]() ,试求
,试求![]() 的值,
的值,

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图1),直接写出线段AD与NE的数量关系为 . 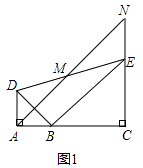
(2)将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),判断△ACN是什么特殊三角形并说明理由.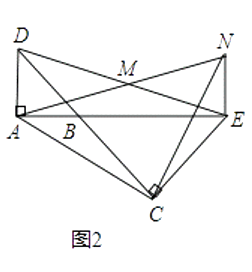
(3)将图1中△BCE绕点B旋转到图3位置,此时A,B,M三点在同一直线上.若AC=3 ![]() ,AD=1,则四边形ACEN的面积为 .
,AD=1,则四边形ACEN的面积为 . 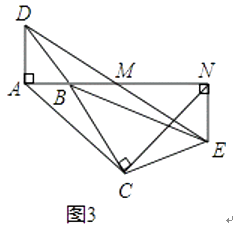
查看答案和解析>>
科目:初中数学 来源: 题型:
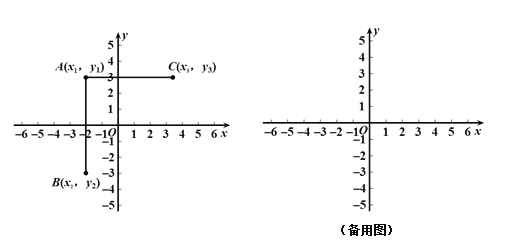
【题目】问题情境:
如图,在平面直角坐标系中有三点A(x1,y1),B(x2,y2),C(x3,y3),小明在学习中发现,当x1=x2,AB∥y轴,线段AB的长度为|y1﹣y2|;当y1=y3,AC∥x轴,线段AC的长度为|x1﹣x3|.
初步应用
(1)若点A(﹣1,1)、B(2,1),则AB∥ 轴(填“x”或“y”);
(2)若点C(1,﹣2),CD∥y轴,且点D在x轴上,则CD= ;
(3)若点E(﹣3,2),点F(t,﹣4),且EF∥y轴,t= ;
拓展探索:
已知P(3,﹣3),PQ∥y轴.
(1)若三角形OPQ的面积为3,求满足条件的点Q的坐标.
(2)若PQ=a,将点Q向右平移b个单位长度到达点M,已知点M在第一象限角平分线上,请直接写出a,b之间满足的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
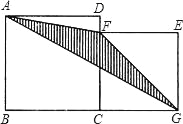
【题目】如图所示,四边形ABCD和CGEF分别是边长为xcm和ycm的正方形,
(1)用含x和y的代数式表示图中阴影部分的面积.
(2)当x=24,y=20时,求此阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
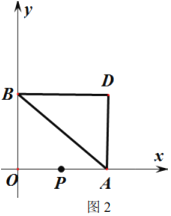
【题目】如图1,在平面直角坐标系中,点![]() 为坐标原点,点
为坐标原点,点![]() 分别在
分别在![]() 轴正半轴和
轴正半轴和![]() 轴正半轴上,且
轴正半轴上,且![]() ,点
,点![]() 从原点出发以每秒
从原点出发以每秒![]() 个单位长度的速度沿x轴正半轴方向运动.
个单位长度的速度沿x轴正半轴方向运动.

(1)求点![]() 的坐标.
的坐标.
(2)连接![]() 设三角形
设三角形![]() 的面积为
的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() ,请用含
,请用含![]() 的式子表示
的式子表示![]() 并直接写出
并直接写出![]() 的取值范围.
的取值范围.
(3)当点![]() 在
在![]() 上运动时,将线段
上运动时,将线段![]() 沿
沿![]() 轴正方向平移,使点
轴正方向平移,使点![]() 与点
与点![]() 重合,点
重合,点![]() 的对应点为点
的对应点为点![]() ,连接
,连接![]() ,将线段
,将线段![]() 沿
沿![]() 轴正方向平移,使点
轴正方向平移,使点![]() 与点
与点![]() 重合,点
重合,点![]() 的对应点为点
的对应点为点![]() ,取
,取![]() 的中点
的中点![]() 是否存在
是否存在![]() 的值,使三角形
的值,使三角形![]() 的面积等于三角形
的面积等于三角形![]() 的面积?若存在,求出
的面积?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
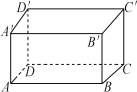
【题目】如图,一只密封的长方体盒子长、宽、高分别为9 cm,3 cm,5 cm,A′处有食物,甲蚂蚁从C处出发沿长方体表面爬行(不能从下底面爬行),乙蚂蚁从B处出发沿B→A→A′方向爬行,问甲蚂蚁是否有先得到食物的可能?并说明理由.(两蚂蚁爬行速度相同)
查看答案和解析>>
科目:初中数学 来源: 题型:
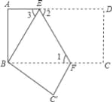
【题目】如图,已知把长方形纸片ABCD沿EF折叠后,点D与点B重合,点C落在点C′的位置上,若∠1=60°,AE=2.
(1)求∠2,∠3的度数.
(2)求长方形ABCD的纸片的面积S.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com