
【题目】某地区为了鼓励市民节约用水,计划实行生活用水按阶梯式水价计费,每月用水量不超过10吨(含10吨)时,每吨按基础价收费;每月用水量超过10吨时,超过的部分每吨按调节价收费.例如,第一个月用水16吨,需交水费17.8元,第二个月用水20吨,需交水费23元.
(1)求每吨水的基础价和调节价
(2)设每月用水量为n吨,应交水费为m元,写出m与n之间的函数解析式;
(3)若某月用水12吨,应交水费多少元?
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.若a∈R,则“ ![]() <1”是“a>1”的必要不充分条件
<1”是“a>1”的必要不充分条件
B.“p∧q为真命题”是“p∨q为真命题”的必要不充分条件
C.若命题p:“?x∈R,sinx+cosx≤ ![]() ”,则¬p是真命题
”,则¬p是真命题
D.命题“?x0∈R,使得x02+2x0+3<0”的否定是“?x∈R,x2+2x+3>0”
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某生在旗杆EF与实验楼CD之间的A处,测得∠EAF=60°,然后向左移动12米到B处,测得∠EBF=30°,∠CBD=45°,sin∠CAD= ![]() .
. 
(1)求旗杆EF的高;
(2)求旗杆EF与实验楼CD之间的水平距离DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形纸片ABCD的边长为1,M、N分别是AD、BC边上的点,且AB∥MN,将纸片的一角沿过点B的直线折叠,使A落在MN上,落点记为A′,折痕交AD于点E,若M是AD边上距D点最近的n等分点(n≥2,且n为整数),则A′N= . 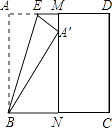
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋装有三个完全相同的小球,分别标号为1、2、3.求下列事件的概率:
(1)从中任取一球,小球上的数字为偶数
(2)从中任取一球,记下数字作为点A的横坐标x,把小球放回袋中,再从中任取一球记下数字作为点A的纵坐标y,点A(x,y)在函数y=![]() 的图象上.
的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校学生的课外阅读情况,随机抽查了10学生周阅读用时数,结果如下表:
周阅读用时数(小时) | 4 | 5 | 8 | 12 |
学生人数(人) | 3 | 4 | 2 | 1 |
则关于这10名学生周阅读所用时间,下列说法正确的是( )
A.中位数是6.5
B.众数是12
C.平均数是3.9
D.方差是6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了弘扬“社会主义核心价值观”,市政府在广场树立公益广告牌,如图所示,为固定广告牌,在两侧加固钢缆,已知钢缆底端D距广告牌立柱距离CD为3米,从D点测得广告牌顶端A点和底端B点的仰角分别是60°和45°.
(1)求公益广告牌的高度AB。
(2)求加固钢缆AD和BD的长.(注意:本题中的计算过程和结果均保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B=45°,∠C=30°,点D是BC上一点,连接AD,过点A作AG⊥AD,在AG上取点F,连接DF.延长DA至E,使AE=AF,连接EG,DG,且GE=DF.
(1)若AB=2 ![]() ,求BC的长;
,求BC的长;
(2)如图1,当点G在AC上时,求证:BD= ![]() CG;
CG;
(3)如图2,当点G在AC的垂直平分线上时,直接写出 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com