
分析 (1)根据方程的系数结合根的判别式即可得出△>0,此题得证;
(2)根据根与系数的关系即可得出x1+x2=-a、x1•x2=a-2,结合$|{x_1}-{x_2}|=\sqrt{13}$即可得出关于a的一元二次方程,解之即可得出a的值.
解答 (1)证明:在方程x2+ax+a-2=0中,△=a2-4(a-2)=(a-2)2+4,
∵(a-2)2≥0,
∴△>0,
故不论a为何实数,此方程总有两个不相等的实数根.
(2)解:∵方程x2+ax+a-2=0的两个实数根分别为x1,x2,
∴x1+x2=-a,x1•x2=a-2,
∵$|{x_1}-{x_2}|=\sqrt{13}$,
∴${({x_1}-{x_2})^2}=13$,
∴${({x_1}+{x_2})^2}-4{x_1}{x_2}=13$,即a2-4(a-2)=13,
整理得:(a-2)2=9,
解得:a1=5,a2=-1.
点评 本题考查了根的判别式以及根与系数的关系,熟练掌握“当△>0时,方程有两个不相等的两个实数根”是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,将抛物线y=2x2沿y轴向上平移1个单位,再沿x轴向右平移2个单位,平移后抛物线的顶点坐标记作A,直线x=3与平移后的抛物线相交于B,与直线OA相交于C.
在平面直角坐标系xOy中,将抛物线y=2x2沿y轴向上平移1个单位,再沿x轴向右平移2个单位,平移后抛物线的顶点坐标记作A,直线x=3与平移后的抛物线相交于B,与直线OA相交于C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
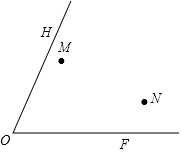 现有M和N两个村庄,欲在其旁两条公路OH、OF上建立A、B两个候车厅,使MA+AB+BN距离最小,请你在OH、OF上确定A、B两点的位置(保留作图痕迹)
现有M和N两个村庄,欲在其旁两条公路OH、OF上建立A、B两个候车厅,使MA+AB+BN距离最小,请你在OH、OF上确定A、B两点的位置(保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com