
【题目】星期天,玲玲骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图像回答下列问题.

(1)玲玲到达离家最远的地方是什么时间?离家多远?
(2)她何时开始第一次休息?休息了多长时间?
(3)她骑车速度最快是在什么时候?车速多少?
(4)玲玲全程骑车的平均速度是多少?
【答案】3小时、30千米;10点休息、半小时;返回途中、15千米/小时;10千米/小时.
【解析】试题分析:本题是一道函数图象的基础题,解题的关键是通过仔细观察图象,从中整理出解题时所需的相关信息,因此本题实际上是考查同学们的识图能力.图中的点的横坐标表示时间,所以点E点距离家最远,横坐标表示距家最远的时间,纵坐标表示离家的距离;休息是路程不在随时间的增加而增加;往返全程中回来时候速度最快,用距离除以所用时间即可;用玲玲全程所行的路程除以所用的时间即可.
试题解析:观察图象可知:(1)玲玲到离家最远的地方需要3小时,此时离家30千米;
(2)10点半时开始第一次休息;休息了半小时;
(3)玲玲在返回的途中最快,速度为:30÷(15﹣13)=15千米/小时;
(4)玲玲全程骑车的平均速度为:(30+30)÷(15﹣9)=10千米/小时.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E,若AB=8,AD=3,则图中阴影部分的周长为( ) 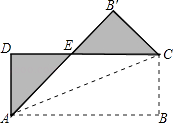
A.16
B.19
C.22
D.25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ACB中,∠C=90°,D是AB上一点,以BD为直径的⊙O与AC相切于点E,交BC于点F,连接DF.
(1)求证:DF=2CE;
(2)若BC=3,sinB=![]() ,求线段BF的长.
,求线段BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习了《相似图形》一章后,小华想测量一座底部不可直接到达的塔DC的高度,上午8点时,测得塔的影子顶端落在地面上的A处,此时小华站在地面上的G处,发现自己的影子顶端落在地面上的E处;上午10点时,测得塔的影子顶端落在地面上的B处,此时站在G处的小华发现自己的影子顶端落在地面上的F处.已知小华身高HG=1.8 m,经测量AB=10 m,FE=0.4 m,求塔DC的高度.
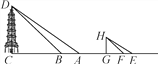
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
发现问题:
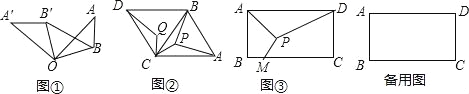
如图①,已知:△OAB中,OB=3,将△OAB绕点O逆时针旋转90°得△OA′B,连接BB′.
则BB′= .
问题探究:
如图②,已知△ABC是边长为4![]() 的等边三角形,以BC为边向外作等边△BCD,P为△ABC内一点,将线段CP绕点C逆时针旋转60°,P的对应点为Q.
的等边三角形,以BC为边向外作等边△BCD,P为△ABC内一点,将线段CP绕点C逆时针旋转60°,P的对应点为Q.
(1)求证:△DCQ≌△BCP
(2)求PA+PB+PC的最小值.
实际应用:
如图③,某货运场为一个矩形场地ABCD,其中AB=500米,AD=800米,顶点A、D为两个出口,现在想在货运广场内建一个货物堆放平台P,在BC边上(含B、C两点)开一个货物入口M,并修建三条专用车道PA、PD、PM.若修建每米专用车道的费用为10000元,当M,P建在何处时,修建专用车道的费用最少?最少费用为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一正方形ABCD中.E为对角线AC上一点,连接EB、ED,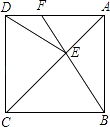
(1)求证:△BEC≌△DEC:
(2)延长BE交AD于点F,若∠DEB=140°.求∠AFE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com