练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

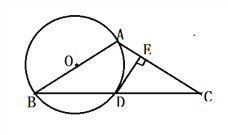
    【题目】已知：如图，在⊿ABC中，AB=AC，以AB为直径的⊙O交BC于点D，过点D作于点E．

    （1）证明：DE是⊙O的切线；

    （2）若，AB＝8，求DE的长．

    【答案】（1）证明见解析；（2）

    【解析】分析：(1)连接OD，证明OD∥AC，得到；(2)连接AD，在直角三角形ABD中求AD，求得∠ADE＝30°，在直角三角形ADE中求DE.

    详解：(1)如图，连接OD，

    ∵AB＝AC，∴∠B＝∠C，

    ∵OB＝OD，∴∠B＝∠ODB，

    ∴∠ODB＝∠C，∴OD∥AC，

    ∵，∴.

    ∵点OD是⊙O的半径，

    ∴DE是⊙O的切线，

    (2)如图，连接AD，所以∠ADB＝90°，

    ∵AB＝AC，所以BD＝CD，∠B＝∠C，

    ∵∠B＝30°，∴AD＝AB＝4，

    ∵∠ADE＋∠EDC＝90°，∠EDC＋∠C＝90°，

    ∴∠ADE＝∠C＝30°，

    ∴AE＝AD＝2，DE＝.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某校八年级两个班，各选派10名学生参加学校举行的“美丽绍兴乡土风情知识”大赛预赛各参赛选手的成绩如下：

    八（1）班：88，91，92，93，93，93，94，98，98，100；

    八（2）班：89，93，93，93，95，96，96，98，98，99．

    通过整理，得到数据分析表如下：

    班级

    最高分

    平均分

    中位数

    众数

    方差

    八（1）班

    100

    m

    93

    93

    12

    八（2）班

    99

    95

    n

    93

    8.4

    （1）求表中m、n的值；

    （2）依据数据分析表，有同学说：“最高分在（1）班，（1）班的成绩比（2）班好”，但也有同学说（2）班的成绩更好请您写出两条支持八（2）班成绩好的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】中国有个名句“运筹帷幄之中，决胜千里之外”．其中的“筹”原意是指《孙子算经》中记载的“算筹”．算筹是古代用来进行计算的工具，它是将几寸长的小竹棍摆在平面上进行运算，算筹的摆放形式有纵横两种形式（如图）．

    当表示一个多位数时，像阿拉伯计数一样，把各个数位的数码从左到右排列，但各位数码的筹式需要纵横相间：个位、百位、万位数用纵式表示；十位，千位，十万位数用横式表示；“0”用空位来代替，以此类推．例如3306用算筹表示就是，则2022用算筹可表示为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一个长方形运动场被分隔成A，B，A，B，C共5个区，A区是边长为a m的正方形，C区是边长为c m的正方形．

    (1)列式表示每个B区长方形场地的周长，并将式子化简；

    (2)列式表示整个长方形运动场的周长，并将式子化简；

    (3)如果a＝40，c＝10，求整个长方形运动场的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是

    A．AB∥DC，AD∥BC　　B．AB=DC，AD=BC

    C．AO=CO，BO=DO　 　D．AB∥DC，AD=BC

    查看答案和解析>>

    科目：初中数学 来源： 题型：

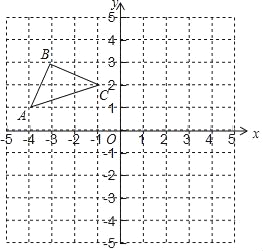
    【题目】如图，在平面直角坐标系中，点O为坐标原点，已知△ABC三个定点坐标分别为A（﹣4，1），B（﹣3，3），C（﹣1，2）．

    （1）画出△ABC关于x轴对称的△A1B1C1，点A，B，C的对称点分别是点A1、B1、C1，直接写出点A1，B1，C1的坐标：A1（　 　，　 　），B1（　 　，　 　），C1（　 　，　 　）；

    （2）画出点C关于y轴的对称点C2，连接C1C2，CC2，C1C，并直接写出△CC1C2的面积是　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

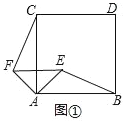
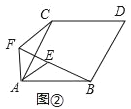
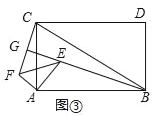
    【题目】（1）如图①，四边形ABDC是正方形，以A为顶点，作等腰直角三角形△AEF，∠EAF=90°，线段BE与CF之间的数量关系为：_____．（直接写出结果，不需要证明）

    （2）如图②，四边形ABDC是菱形，以A为顶点，作等腰三角形△AEF，AE=AF，∠BAC=∠EAF，（1）中结论成立吗？若成立，请证明；若不成立，请说明理由．

    （3）如图③，四边形ABDC是矩形，以A为顶点，作直角三角形△AEF，∠EAF=90°，AB=AC，AE=AF，当∠EAB=60°时，延长BE交CF于点G．

    ①求证：BE⊥CF；

    ②当AB=12，AE=4时，求线段BG的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在平面直角坐标系xOy中，A(a，0)、B(0，b)、C(﹣a，0)，且+b2﹣4b+4＝0

    (1)求证：∠ABC＝90°；

    (2)作∠ABO的平分线交x轴于一点D，求D点的坐标；

    (3)如图2所示，A、B两点在x轴、y轴上的位置不变，在线段AB上有两动点M、N，满足∠MON＝45°，下列结论：①BM+AN＝MN；②BM2+AN2＝MN2，其中有且只有一个结论成立．请你判断哪一个结论成立，并证明成立的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

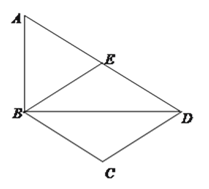
    【题目】如图，在Rt△ABD中，∠ABD=90°，AB=1，sin∠ADB=，点E为AD的中点，线段BA绕点B顺时针旋转到BC（旋转角小于180°），使BC∥AD．连接DC，BE．

    （1）则四边形BCDE是________，并证明你的结论；

    （2）求线段AB旋转过程中扫过的面积．

    查看答案和解析>>

    同步练习册答案