
����Ŀ����֪���ڡ�ABC�У�AB=AC����A���ֱ��a�����AC�غϵ�λ�ÿ�ʼ�Ƶ�A��˳ʱ�뷽����ת�Ǧȣ�ֱ��a��BC���ڵ�P����P�����B����C�غϣ�����BMN�ı�MNʼ����ֱ��a�ϣ���M�ڵ�N���Ϸ�������BM=BN������CN�� 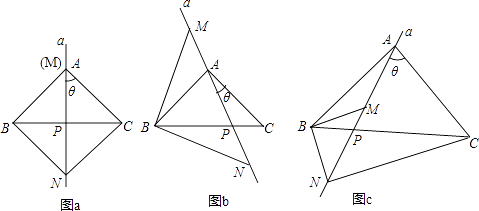
��1������BAC=��MBN=90��ʱ�� ����ͼa������=45��ʱ����ANC�Ķ���Ϊ��
��2������ͼb�����ȡ�45��ʱ�����еĽ����Ƿ����仯��˵�����ɣ�
��3����ͼc������BAC=��MBN��90��ʱ����ֱ��д����ANC���BAC֮���������ϵ������֤����
���𰸡�
��1��45��
��2���⣺����CN�����ȡ�45��ʱ�����еĽ��۲������仯��
�������£��ߡ�BAC=��MBN=90�㣬AB=AC��BM=BN��
���ABC=��ACB=��BNP=45�㣬
�֡ߡ�BPN=��APC��
���BNP�ס�ACP��
�� ![]() =
= ![]() ��
��
�֡ߡ�APB=��CPN��
���ABP�ס�CNP��
���ANC=��ABC=45��
��3����ANC=90�㩁 ![]() ��BAC��
��BAC��
�������£��ߡ�BAC=��MBN��90�㣬AB=AC��BM=BN��
���ABC=��ACB=��BNP= ![]() ��180�㩁��BAC����
��180�㩁��BAC����
�֡ߡ�BPN=��APC��
���BNP�ס�ACP��
�� ![]() =
= ![]() ��
��
�֡ߡ�APB=��CPN��
���ABP�ס�CNP��
���ANC=��ABC��
�ڡ�ABC�У���ABC= ![]() ��180�㩁��BAC��=90�㩁
��180�㩁��BAC��=90�㩁 ![]() ��BAC
��BAC
���������⣺��1���١ߡ�BAC=90�㣬��=45�㣬 ��AP��BC��BP=CP���������������ߺ�һ����
��AP=BP��ֱ��������б���ϵ����ߵ���б�ߵ�һ�룩��
�֡ߡ�MBN=90�㣬BM=BN��
��AP=PN���������������ߺ�һ����
��AP=PN=BP=PC����AN��BC��
���ı���ABNC�������Σ�
���ANC=45�㣻��1����֤���ı���ABNC�������Σ����������εĶԽ���ƽ��һ��Խ�������⣻�ڸ��ݵ���ֱ�������ε����ʿɵá�BNP=��ACB��Ȼ��֤����BNP�͡�ACP���ƣ��������������ζ�Ӧ�߳ɱ����ɵ� ![]() =
= ![]() ���ٸ������߶�Ӧ�ɱ����н���ȿɵá�ABP�͡�CNP���ƣ�Ȼ��������������ζ�Ӧ����ȿɵá�ANC=��ABC���Ӷ��ý⣻��3�����ݵ��������ε�������������BNP=��ACB��Ȼ��֤����BNP�͡�ACP���ƣ��������������ζ�Ӧ�߳ɱ����ɵ�
���ٸ������߶�Ӧ�ɱ����н���ȿɵá�ABP�͡�CNP���ƣ�Ȼ��������������ζ�Ӧ����ȿɵá�ANC=��ABC���Ӷ��ý⣻��3�����ݵ��������ε�������������BNP=��ACB��Ȼ��֤����BNP�͡�ACP���ƣ��������������ζ�Ӧ�߳ɱ����ɵ� ![]() =
= ![]() ���ٸ������߶�Ӧ�ɱ����н���ȿɵá�ABP�͡�CNP���ƣ�Ȼ��������������ζ�Ӧ����ȿɵá�ANC=��ABC��Ȼ����������ε��ڽǺͶ�����ʽ�������ɵý⣮
���ٸ������߶�Ӧ�ɱ����н���ȿɵá�ABP�͡�CNP���ƣ�Ȼ��������������ζ�Ӧ����ȿɵá�ANC=��ABC��Ȼ����������ε��ڽǺͶ�����ʽ�������ɵý⣮


 ����ѧ��Ӯ�����ϵ�д�
����ѧ��Ӯ�����ϵ�д� ѧ���쳵�����ּ��������ҵ�½����������ϵ�д�
ѧ���쳵�����ּ��������ҵ�½����������ϵ�д� �����ѧСѧ�꼶�νӵ������㽭��ѧ������ϵ�д�
�����ѧСѧ�꼶�νӵ������㽭��ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ƽ��ֱ������ϵxOy�У���A��4��0����������y=ax2+2x��c�ϵ�һ�㣬��������������ƽ��6����λ����B��0��2����ƽ�ƺ����õ��������ߵĶ����ΪC���������ߵĶԳ������߶�AB�Ľ����ΪP��
��1����ƽ�ƺ����õ����������ߵı���ʽ����д����C�����ꣻ
��2�����CAB������ֵ��
��3�������Q���������߶Գ����ϵ�һ�㣬�ҡ�BCQ���ACP���ƣ����Q�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�н������Ϣ������ҵ���ԣ�����ѧ����ǩ�ķ�ʽ�����Լ��Ŀ������ݣ��涨��ÿλ�����������������⣨��ǩ�ֱ��ô���B1��B2��B3��ʾ���г�ȡһ�������������ϻ��⣨��ǩ�ֱ��ô���J1��J2��J3��ʾ���г�ȡһ�����п��ԣ�С���ڿ�������ǩ������£��ֱ�ӱ�������ϻ���������س�ȡһ����ǩ��
��1������״ͼ���б�����ʾ�����п��ܵĽ����
��2����С���鵽�ı�������ϻ������ǩ������±꣨���硰B1�����±�Ϊ��1����Ϊһ������һ��ż���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����1�������1��������130Ԫ������2�������3��������340Ԫ��
��1����ÿ�������ÿ��������ۼۣ�
��2�����ijУ�ƻ�������������54�����ܷ��ò�����4000Ԫ������������ٸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�ǡ�ABC�����Բ��AC��ֱ������E��AB���е㣬�ӳ�EO����O��D�㣬��BC=DC��AB=2 ![]() ����
���� ![]() �ij��ȣ�
�ij��ȣ� 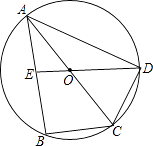
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ��ֱ��Ϊ24cm��Բ��ֽƬ�ϼ���һ��Բ�Ľ�Ϊ90�������ABC��ʹ��A��B��C��Բ���ϣ������µ�������Ϊһ��Բ�IJ��棬�����Բ�ĵ���Բ�İ뾶�ǣ�������
A.12cm
B.6cm
C.3 ![]() cm
cm
D.2 ![]() cm
cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������
��1�����䷽����һԪ���η��̣�x2��6x+4=0��
��2����֪����x��һԪ���η���x2��4x+m=0�ĸ����б�ʽ��ֵΪ4����mֵ�����̵ĸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����б�߳�Ϊ4��ֱ�����ǰ����ֱ������ϵxOy�У�����ֱ�DZ߷ֱ����������غϣ�PΪб�ߵ��е㣮�ֽ������ǰ��Ƶ�O˳ʱ����ת120����P�Ķ�Ӧ��������ǣ� ��
A.�� ![]() ��1��
��1��
B.��1���� ![]() ��
��
C.��2 ![]() ����2��
����2��
D.��2����2 ![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com