
【题目】如图,⊙O是△ABC的外接圆,AC是直径,点E是AB的中点,延长EO交⊙O于D点,若BC=DC,AB=2 ![]() ,求
,求 ![]() 的长度.
的长度. 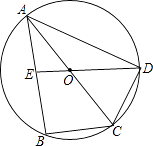
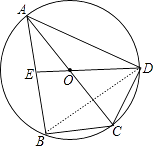
【答案】解:连结BD,如图, ∵BC=DC,
∴ ![]() =
= ![]() ,
,
∴AC垂直平分BD,
∴AB=AD,
∵点E是AB的中点,即AE=BE= ![]() ,
,
∴DE⊥AB,
∴DA=DB,
∴AB=AD=DB,
∴△ABD为等边三角形,
∴∠BAC=30°,∠ABD=60°,
∴∠AOD=2∠ABD=120°,
在Rt△AEO中,∵∠EAO=30°,
∴OE= ![]() AE=1,AO=2OE=2,
AE=1,AO=2OE=2,
∴ ![]() 的长度=
的长度= ![]() =
= ![]() .
.
【解析】连结BD,如图,利用圆心角、弧、弦的关系,由BC=DC得 ![]() =
= ![]() ,则根据垂径定理得到AC垂直平分BD,所以AB=AD,同样可得DA=DB,则可判断△ABD为等边三角形,所以∠BAC=30°,∠ABD=60°,根据圆周角定理得∠AOD=2∠ABD=120°,然后在Rt△AEO中计算出AO,最后利用弧长公式计算即可.
,则根据垂径定理得到AC垂直平分BD,所以AB=AD,同样可得DA=DB,则可判断△ABD为等边三角形,所以∠BAC=30°,∠ABD=60°,根据圆周角定理得∠AOD=2∠ABD=120°,然后在Rt△AEO中计算出AO,最后利用弧长公式计算即可.
【考点精析】通过灵活运用三角形的外接圆与外心和弧长计算公式,掌握过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心;若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的即可以解答此题.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】2016年3月完工的上海中心大厦是一座超高层地标式摩天大楼,其高度仅次于世界排名第一的阿联酋迪拜大厦,某人从距离地面高度263米的东方明珠球体观光层测得上海中心大厦顶部的仰角是22.3°.已知东方明珠与上海中心大厦的水平距离约为900米,那么上海中心大厦的高度约为米(精确到1米).(参考数据:sin22.3°≈0.38,cos22.3°≈0.93.tan22.3°≈0.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农业现代化是我国“十三五”的重要规划之一,某地农民积极响应政府号召,自发成立现代新型农业合作社,适度扩大玉米种业规模,今年,合作社600亩玉米喜获丰收.合作社打算雇佣玉米收割机收割玉米,现有A,B两种型号收割机可供选择,且每台B种型号收割机每天的收个亩数是A种型号的1.5倍,如果单独使用一台收割机将600亩玉米全部收割完,A种型号收割机比B种型号收割机多用10天. 
(1)求A,B两种型号收割机每台每天收个玉米的亩数;
(2)已知A种型号收割机收费是45元/亩,B种型号收割机收费是50元/亩,经过研究,合作社计划同时雇佣A,B两种型号收割机各一台合作完成600亩玉米的收割任务,则合作社需要支付的玉米收割总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA、PB是⊙O的切线,A、B是切点,点C是劣弧AB上的一个动点,若∠ACB=110°,则∠P的度数是( ) 
A.55°
B.30°
C.35°
D.40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,AB=AC.过A点的直线a从与边AC重合的位置开始绕点A按顺时针方向旋转角θ,直线a交BC边于点P(点P不与点B、点C重合),△BMN的边MN始终在直线a上(点M在点N的上方),且BM=BN,连接CN. 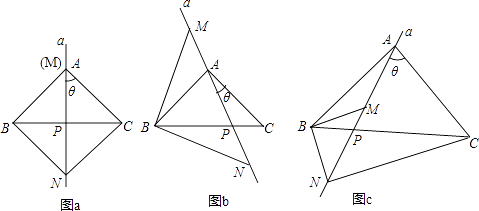
(1)当∠BAC=∠MBN=90°时, ①如图a,当θ=45°时,∠ANC的度数为;
(2)②如图b,当θ≠45°时,①中的结论是否发生变化?说明理由;
(3)如图c,当∠BAC=∠MBN≠90°时,请直接写出∠ANC与∠BAC之间的数量关系,不必证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=x2+mx的对称轴是x=3,则关于x的方程x2+mx=7的解为( )
A.x1=0,x2=6
B.x1=1,x2=7
C.x1=1,x2=﹣7
D.x1=﹣1,x2=7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】秋季新学期开学时,红城中学对七年级新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格,现学校随机选取了部分学生的成绩,整理并制作成了如下不完整的图表:
分 数 段 | 频数 | 频率 |
60≤x<70 | 9 | a |
70≤x<80 | 36 | 0.4 |
80≤x<90 | 27 | b |
90≤x≤100 | c | 0.2 |

请根据上述统计图表,解答下列问题:
(1)在表中,a= , b= , c=;
(2)补全频数直方图;
(3)根据以上选取的数据,计算七年级学生的平均成绩.
(4)如果测试成绩不低于80分者为“优秀”等次,请你估计全校七年级的800名学生中,“优秀”等次的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,△DCE,△FEG是三个全等的等腰三角形,底边BC,CE,EG在同一直线上,且AB= ![]() ,BC=1,连结BF,分别交AC,DC,DE于点P,Q,R.
,BC=1,连结BF,分别交AC,DC,DE于点P,Q,R.
(1)求证:△BFG∽△FEG,并求出BF的长;
(2)求AP:PC的值;
(3)观察图形,请你提出一个与点P相关的问题,并进行解答.(根据提出问题的层次和解答过程平分)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,并绘制出扇形统计图和频数分布直方图(不完整).规定x≥6.25为合格,x≥9.25为优秀. 
(1)这部分男生有多少人?其中成绩合格的有多少人?
(2)这部分男生成绩的中位数落在哪一组?扇形统计图中D组对应的圆心角是多少度?
(3)要从成绩优秀的学生中,随机选出2人介绍经验,已知甲、乙两位同学的成绩均为优秀,求他俩至少有1人被选中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com