
【题目】有一个圆形转盘,分黑色、白色两个区域.
(1)某人转动转盘,对指针落在黑色区域或白色区域进行了大量试验,得到数据如下表:
实验次数 | 10 | 100 | 2000 | 5000 | 10000 | 50000 | 100000 |
白色区域次数 | 3 | 34 | 680 | 1600 | 3405 | 16500 | 33000 |
落在白色区域频率 | 0.3 | 0.34 | 0.34 | 0.32 | 0.34 | 0.33 | 0.33 |
请你利用上述实验,估计转动该转盘指针落在白色区域的概率为___________.(精确到0.01);
(2)若该圆形转盘白色扇形的圆心角为120度,黑色扇形的圆心角为![]() ,转动转盘两次,求指针一次落在白色区域,另一次落在黑色区域的概率.
,转动转盘两次,求指针一次落在白色区域,另一次落在黑色区域的概率.
【答案】(1)0.33;(2)![]() .
.
【解析】
(1)根据实验得到的数据,可以求这几次实验概率的平均值,即可估算出来;
(2)根据红白所对应的圆心角度数,可以知道红白分别所占圆心角的比例,并按照比例划分,列举出所有情况,根据概率=所求情况数与总情况数之比,即可求解.
(1)根据7次实验的结果,落在白色区域的概率分别是0.3、0.34、0.34、0.32、0.34、0.33、0.33,
所以这几次实验的平均数是(0.3+0.34+0.34+0.32+0.34+0.33+0.33)÷7≈0.33,
故转动该转盘指针落在白色区域的概率为0.33.
(2)![]() 白色扇形的圆心角为120°,占一个圆的三分之一,黑色扇形的圆心角为
白色扇形的圆心角为120°,占一个圆的三分之一,黑色扇形的圆心角为![]() ,占一个圆的三分之二,因此,把一个圆平均分成三份;
,占一个圆的三分之二,因此,把一个圆平均分成三份;
![]() 设白色扇形区域为白,黑色扇形区域为黑1、黑2,可得下面的图表:
设白色扇形区域为白,黑色扇形区域为黑1、黑2,可得下面的图表:
列表:

从列表可知:共有9种等可能的结果,其中指针一次落在白色区域,另一次落在黑色区域的有4种,分别为:(白,黑1),(白,黑2),(黑1,白),(黑2,白).
![]() (一白一黑)
(一白一黑)![]() .
.
答:指针一次落在白色区域,另一次落在黑色区域的概率为![]() .
.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
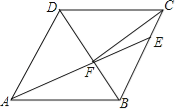
【题目】如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,CE=2,连接CF,以下结论:①△ABF≌△CBF;②点E到AB的距离是2![]() ;③tan∠DCF=
;③tan∠DCF=![]() ;④△ABF的面积为
;④△ABF的面积为![]() .其中一定成立的是 (把所有正确结论的序号都填在横线上).
.其中一定成立的是 (把所有正确结论的序号都填在横线上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是![]() 的中点,连接AC并延长至点D,使CD=AC,点E是OB上一点,且
的中点,连接AC并延长至点D,使CD=AC,点E是OB上一点,且![]() ,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.
,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.

(1)求证:BD是⊙O的切线;(2)当OB=2时,求BH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
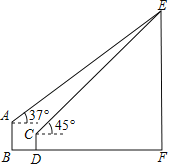
【题目】如图,甲楼AB高20米,乙楼CD高10米,两栋楼之间的水平距离BD=30m,为了测量某电视塔EF的高度,小明在甲楼楼顶A处观测电视塔塔顶E,测得仰角为37°,小明在乙楼楼顶C处观测电视塔塔顶E,测得仰角为45°,求该电视塔的高度EF.
(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
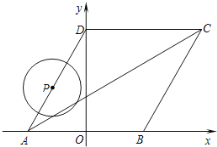
【题目】如图所示,菱形ABCD的顶点A、B在![]() 轴上,点A在点B的左侧,点D在
轴上,点A在点B的左侧,点D在![]() 轴的正半轴上,
轴的正半轴上,![]() ,点A的坐标为
,点A的坐标为![]() .
.
(1)求D点的坐标.
(2)求直线AC的函数关系式.
(3)动点P从点A出发,以每秒1个单位长度的速度,按照![]() 的顺序在菱形的边上匀速运动一周,设运动时间为
的顺序在菱形的边上匀速运动一周,设运动时间为![]() 秒.求
秒.求![]() 为何值时,以点P为圆心、以1为半径的圆与对角线AC相切?
为何值时,以点P为圆心、以1为半径的圆与对角线AC相切?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 与
与![]() 轴交于点
轴交于点![]() ,将点
,将点![]() 向右平移两个单位长度,得到点
向右平移两个单位长度,得到点![]() ,点
,点![]() 在抛物线上.
在抛物线上.
(1)①直接写出抛物线的对称轴是__________;
②用含![]() 的代数式表示
的代数式表示![]() ;
;
(2)横、纵坐标都是整数的点叫做整点.点![]() 恰好为整点,若抛物线在点
恰好为整点,若抛物线在点![]() 、
、![]() 之间的部分与线段
之间的部分与线段![]() 所围成的区域内(不含边界)恰有两个整点,结合函数图象,求
所围成的区域内(不含边界)恰有两个整点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AO⊥BC于点O,OE⊥AB于点E,以点O为圆心,OE为半径作半圆,交AO于点F.
(1)求证:AC是⊙O的切线;
(2)若点F是OA的中点,OE=3,求图中阴影部分的面积;
(3)在(2)的条件下,点P是BC边上的动点,当PE+PF取最小值时,直接写出BP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
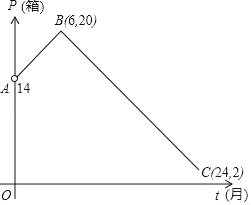
【题目】某竹制品加工厂根据市场调研结果,对该厂生产的一种新型竹制品玩具未来两年的销售进行预测,并建立如下模型:设第t个月,竹制品销售量为P(单位:箱),P与t之间存在如图所示函数关系,其图象是线段AB(不含点A)和线段BC的组合.设第t个月销售每箱的毛利润为Q(百元),且Q与t满足如下关系Q=2t+8(0≤t≤24).
(1)求P与t的函数关系式(6≤t≤24).
(2)该厂在第几个月能够获得最大毛利润?最大毛利润是多少?
(3)经调查发现,当月毛利润不低于40000且不高于43200元时,该月产品原材料供给和市场售最和谐,此时称这个月为“和谐月”,那么,在未来两年中第几个月为和谐月?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com