
【题目】在平面直角坐标系中,![]() 与
与![]() 轴交于点
轴交于点![]() ,将点
,将点![]() 向右平移两个单位长度,得到点
向右平移两个单位长度,得到点![]() ,点
,点![]() 在抛物线上.
在抛物线上.
(1)①直接写出抛物线的对称轴是__________;
②用含![]() 的代数式表示
的代数式表示![]() ;
;
(2)横、纵坐标都是整数的点叫做整点.点![]() 恰好为整点,若抛物线在点
恰好为整点,若抛物线在点![]() 、
、![]() 之间的部分与线段
之间的部分与线段![]() 所围成的区域内(不含边界)恰有两个整点,结合函数图象,求
所围成的区域内(不含边界)恰有两个整点,结合函数图象,求![]() 的取值范围.
的取值范围.
【答案】(1)①直线x=-1;②b=-2a;(2)a的取值范围是![]() 或
或![]() .
.
【解析】
(1)①先求出点A的坐标得到点B的坐标,根据对称性即可得到对称轴;
②根据对称轴的公式计算即可得到;
(2)分两种情况:a>0或a<0,画出图形列不等式组求解.
(1)①当x=0时,得到y=-c,
∴点A的坐标为(0,-c),
∵将点![]() 向右平移两个单位长度,得到点
向右平移两个单位长度,得到点![]() ,
,
∴B(-2,-c),
∵点![]() 在抛物线上,
在抛物线上,
∴抛物线的对称轴是直线x=![]() =-1,
=-1,
故答案为:直线x=-1;
②∵对称轴是x=![]() =-1,
=-1,
∴b=-2a;
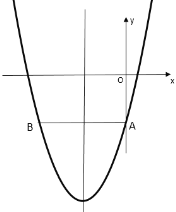
(2)如图,当a>0时,
∵A(0,-c),B(-2,-c),且指定区域内有两个整点,因此整点坐标必为(-1,-c-1)及(-1,-c-2),
∵抛物线的顶点坐标为(-1,-c-a),
∴![]() ,
,
解得![]() ;
;
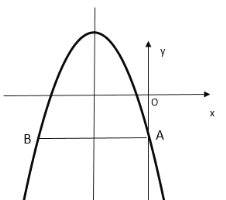
当a<0时,整点坐标必为(-1,-c+1)及(-1,-c+2)此两点必在区域内,
同理可得![]() ,
,
解得![]() ,
,
综上,a的取值范围是![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】某校数学兴趣小组的同学测量一架无人飞机P的高度,如图,A,B两个观测点相距![]() ,在A处测得P在北偏东71°方向上,同时在B处测得P在北偏东35°方向上.求无人飞机P离地面的高度.(结果精确到1米,参考数据:
,在A处测得P在北偏东71°方向上,同时在B处测得P在北偏东35°方向上.求无人飞机P离地面的高度.(结果精确到1米,参考数据:![]() ,
,![]() ,sin71°≈0.95,tan71°≈2.90)
,sin71°≈0.95,tan71°≈2.90)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为4,2,反比例函数y![]() (x>0)的图象经过A,B两点,若菱形ABCD的面积为2
(x>0)的图象经过A,B两点,若菱形ABCD的面积为2![]() ,则k的值为( )
,则k的值为( )
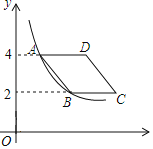
A. 2B. 3C. 4D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个圆形转盘,分黑色、白色两个区域.
(1)某人转动转盘,对指针落在黑色区域或白色区域进行了大量试验,得到数据如下表:
实验次数 | 10 | 100 | 2000 | 5000 | 10000 | 50000 | 100000 |
白色区域次数 | 3 | 34 | 680 | 1600 | 3405 | 16500 | 33000 |
落在白色区域频率 | 0.3 | 0.34 | 0.34 | 0.32 | 0.34 | 0.33 | 0.33 |
请你利用上述实验,估计转动该转盘指针落在白色区域的概率为___________.(精确到0.01);
(2)若该圆形转盘白色扇形的圆心角为120度,黑色扇形的圆心角为![]() ,转动转盘两次,求指针一次落在白色区域,另一次落在黑色区域的概率.
,转动转盘两次,求指针一次落在白色区域,另一次落在黑色区域的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
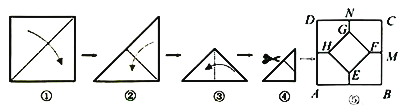
【题目】将一张正方形纸片按如图步骤,通过折叠得到图④,再沿虚线剪去一个角,展开铺平后得到图⑤,其中![]() 是折痕.若正方形
是折痕.若正方形![]() 与五边形
与五边形![]() 的面积相等,则
的面积相等,则![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+(2m﹣1)x﹣2m(m>0.5)的最低点的纵坐标为﹣4.
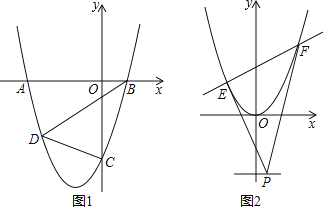
(1)求抛物线的解析式;
(2)如图1,抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,D为抛物线上的一点,BD平分四边形ABCD的面积,求点D的坐标;
(3)如图2,平移抛物线y=x2+(2m﹣1)x﹣2m,使其顶点为坐标原点,直线y=﹣2上有一动点P,过点P作两条直线,分别与抛物线有唯一的公共点E、F(直线PE、PF不与y轴平行),求证:直线EF恒过某一定点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线![]() 与抛物线
与抛物线![]() 的形状相同,开口方向相反,且相交于点
的形状相同,开口方向相反,且相交于点![]() 和点
和点![]() .抛物线
.抛物线![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() 为抛物线
为抛物线![]() 上
上![]() 两点间一动点,过点
两点间一动点,过点![]() 作直线
作直线![]() 轴,与
轴,与![]() 交于点
交于点![]() .
.
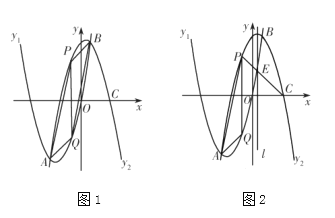
(1)求抛物线![]() 与抛物线
与抛物线![]() 的解析式;
的解析式;
(2)四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值,并写出此时点
的最大值,并写出此时点![]() 的坐标;
的坐标;
(3)如图2,![]() 的对称轴为直线
的对称轴为直线![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,在(2)的条件下,直线
,在(2)的条件下,直线![]() 上是否存在一点
上是否存在一点![]() ,使得以
,使得以![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?如果存在,求出点
相似?如果存在,求出点![]() 的坐标;如果不存在,说明理由.
的坐标;如果不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com