
ЎѕМвДїЎїИзНј1Ј¬ТСЦЄЕЧОпПЯ![]() УлЕЧОпПЯ
УлЕЧОпПЯ![]() µДРОЧґПаН¬Ј¬їЄїЪ·ЅПтПа·ґЈ¬ЗТПаЅ»УЪµг
µДРОЧґПаН¬Ј¬їЄїЪ·ЅПтПа·ґЈ¬ЗТПаЅ»УЪµг![]() єНµг
єНµг![]() Ј®ЕЧОпПЯ
Ј®ЕЧОпПЯ![]() Ул
Ул![]() ЦбХэ°лЦбЅ»УЪµг
ЦбХэ°лЦбЅ»УЪµг![]() ОЄЕЧОпПЯ
ОЄЕЧОпПЯ![]() ЙП
ЙП![]() БЅµгјдТ»¶ЇµгЈ¬№эµг
БЅµгјдТ»¶ЇµгЈ¬№эµг![]() ЧчЦ±ПЯ
ЧчЦ±ПЯ![]() ЦбЈ¬Ул
ЦбЈ¬Ул![]() Ѕ»УЪµг
Ѕ»УЪµг![]() Ј®
Ј®
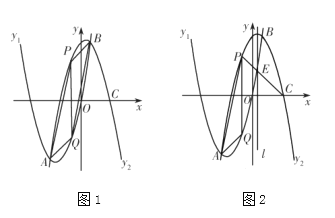
ЈЁ1Ј©ЗуЕЧОпПЯ![]() УлЕЧОпПЯ
УлЕЧОпПЯ![]() µДЅвОцКЅ;
µДЅвОцКЅ;
ЈЁ2Ј©ЛД±ЯРО![]() µДГж»эОЄ
µДГж»эОЄ![]() Ј¬Зу
Ј¬Зу![]() µДЧоґуЦµЈ¬ІўРґіцґЛК±µг
µДЧоґуЦµЈ¬ІўРґіцґЛК±µг![]() µДЧш±к;
µДЧш±к;
ЈЁ3Ј©ИзНј2Ј¬![]() µД¶ФіЖЦбОЄЦ±ПЯ
µД¶ФіЖЦбОЄЦ±ПЯ![]() Ј¬
Ј¬![]() Ул
Ул![]() Ѕ»УЪµг
Ѕ»УЪµг![]() Ј¬ФЪ(2)µДМхјюПВЈ¬Ц±ПЯ
Ј¬ФЪ(2)µДМхјюПВЈ¬Ц±ПЯ![]() ЙПКЗ·сґжФЪТ»µг
ЙПКЗ·сґжФЪТ»µг![]() Ј¬К№µГТФ
Ј¬К№µГТФ![]() ОЄ¶ҐµгµДИэЅЗРОУл
ОЄ¶ҐµгµДИэЅЗРОУл![]() ПаЛЖЈїИз№ыґжФЪЈ¬Зуіцµг
ПаЛЖЈїИз№ыґжФЪЈ¬Зуіцµг![]() µДЧш±кЈ»Из№ыІ»ґжФЪЈ¬ЛµГчАнУЙ.
µДЧш±кЈ»Из№ыІ»ґжФЪЈ¬ЛµГчАнУЙ.
Ўѕґр°ёЎїЈЁ1Ј©![]() Ј»
Ј»![]() Ј»ЈЁ2Ј©16Ј»ЈЁ-1,4Ј©Ј» ЈЁ3Ј©ґжФЪµг
Ј»ЈЁ2Ј©16Ј»ЈЁ-1,4Ј©Ј» ЈЁ3Ј©ґжФЪµг![]() µДЧш±к
µДЧш±к![]() »тЈЁ
»тЈЁ![]() К№µГ
К№µГ![]() ОЄ¶ҐµгµДИэЅЗРОУл
ОЄ¶ҐµгµДИэЅЗРОУл![]() ПаЛЖЈ¬АнУЙјыЅвОцЈ®
ПаЛЖЈ¬АнУЙјыЅвОцЈ®
ЎѕЅвОцЎї
ЈЁ1Ј©·Ц±рАыУГґэ¶ЁПµКэ·ЁЗуБЅёц¶юґОєЇКэµДЅвОцКЅЈ»
ЈЁ2Ј©ЙиµгPєбЧш±кОЄtЈ¬ФтPЈЁtЈ¬t2Ј«tЈ«6Ј©Ј¬QЈЁtЈ¬t2Ј«5tЈ©Ј¬±нКѕPQµДі¤Ј¬ёщѕЭБЅИэЅЗРОГж»эєНїЙµГSУлtµД№ШПµКЅЈ¬Ед·ЅєуїЙµГSµДЧоґуЦµЈ»
ЈЁ3Ј©ПИИ·¶ЁЎПAQBЈЅ135ЎгЈ¬И»єу·ЦБЅЦЦЗйїцМЦВЫїЙµГЅбВЫЈ®
ЅвЈєЈЁ1Ј©Ѕ«![]() ґъИл
ґъИл![]() µГЈє
µГЈє![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
ЎЯ![]() Ул
Ул![]() РОЧґПаН¬Ј¬їЄїЪПа·ґЈ¬
РОЧґПаН¬Ј¬їЄїЪПа·ґЈ¬
Ўа![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
Ѕ«![]() ґъИлµГЈ¬
ґъИлµГЈ¬
![]()
ЅвµГЈє![]() Ј¬
Ј¬![]() Ј¬
Ј¬
Ўа![]() Ј»
Ј»
ЈЁ2Ј©Йиµг![]() єбЧш±кОЄtЈ¬
єбЧш±кОЄtЈ¬
Фт![]() Ј¬
Ј¬![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
Ўа![]()
![]() Ј¬
Ј¬
Ўаµ±![]() К±Ј¬
К±Ј¬![]() Ј¬ґЛК±
Ј¬ґЛК±![]() µДЧш±кОЄ
µДЧш±кОЄ![]() Ј»
Ј»
ЈЁ3Ј©ґжФЪµг![]() Ј¬
Ј¬
УЙ![]() µГЦ±ПЯ
µГЦ±ПЯ![]() ОЄЈє
ОЄЈє![]() Ј¬
Ј¬
УЙЈЁ2Ј©ЦЄ![]() µгµДЧш±кОЄ
µгµДЧш±кОЄ![]() µгµДЧш±кОЄ
µгµДЧш±кОЄ![]() Ј¬
Ј¬
ЗТ![]() ОЄ
ОЄ![]() ,
,
Бо![]() µГЈє
µГЈє![]() ОЄ
ОЄ![]() Ј¬
Ј¬
ИзНјЈ¬Йи![]() Ул
Ул![]() ЦбЅ»УЪµг
ЦбЅ»УЪµг![]() Ј¬Ц±ПЯ
Ј¬Ц±ПЯ![]() Ул
Ул![]() ЦбЅ»УЪµг
ЦбЅ»УЪµг![]() Ј¬
Ј¬
Чч![]() µДСУі¤ПЯЈ¬ґ№ЧгОЄµг
µДСУі¤ПЯЈ¬ґ№ЧгОЄµг![]() Ј¬ТЧЦЄ
Ј¬ТЧЦЄ![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
ЎЯ![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
Ўа![]() µгФЪ
µгФЪ![]() µДЙП·Ѕ
µДЙП·Ѕ![]() Ј¬
Ј¬
![]() Ј¬
Ј¬ ![]() Ј¬
Ј¬
![]() ,
,![]() Ј¬
Ј¬
ўЩИф![]() Ј¬Фт
Ј¬Фт![]() Ј¬
Ј¬
јґ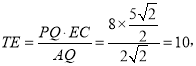
ґЛК±![]() µДЧш±кОЄ
µДЧш±кОЄ![]() Ј»
Ј»
ўЪИф![]() Ј¬Фт
Ј¬Фт![]() Ј¬
Ј¬
јґ![]() Ј¬ґЛК±
Ј¬ґЛК±![]() µДЧш±кОЄ
µДЧш±кОЄ![]() Ј¬
Ј¬
ЧЫЙПїЙЦЄґжФЪµг![]() µДЧш±к
µДЧш±к![]() »тЈЁ
»тЈЁ![]() К№µГ
К№µГ![]() ОЄ¶ҐµгµДИэЅЗРОУл
ОЄ¶ҐµгµДИэЅЗРОУл![]() ПаЛЖЈ®
ПаЛЖЈ®



| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФЪЖЅГжЦ±ЅЗЧш±кПµЦРЈ¬![]() Ул
Ул![]() ЦбЅ»УЪµг
ЦбЅ»УЪµг![]() Ј¬Ѕ«µг
Ј¬Ѕ«µг![]() ПтУТЖЅТЖБЅёцµҐО»і¤¶ИЈ¬µГµЅµг
ПтУТЖЅТЖБЅёцµҐО»і¤¶ИЈ¬µГµЅµг![]() Ј¬µг
Ј¬µг![]() ФЪЕЧОпПЯЙПЈ®
ФЪЕЧОпПЯЙПЈ®
ЈЁ1Ј©ўЩЦ±ЅУРґіцЕЧОпПЯµД¶ФіЖЦбКЗ__________Ј»
ўЪУГє¬![]() µДґъКэКЅ±нКѕ
µДґъКэКЅ±нКѕ![]() Ј»
Ј»
ЈЁ2Ј©єбЎўЧЭЧш±к¶јКЗХыКэµДµгЅРЧцХыµгЈ®µг![]() ЗЎєГОЄХыµгЈ¬ИфЕЧОпПЯФЪµг
ЗЎєГОЄХыµгЈ¬ИфЕЧОпПЯФЪµг![]() Ўў
Ўў![]() Ц®јдµДІї·ЦУлПЯ¶О
Ц®јдµДІї·ЦУлПЯ¶О![]() ЛщО§іЙµДЗшУтДЪЈЁІ»є¬±ЯЅзЈ©ЗЎУРБЅёцХыµгЈ¬ЅбєПєЇКэНјПуЈ¬Зу
ЛщО§іЙµДЗшУтДЪЈЁІ»є¬±ЯЅзЈ©ЗЎУРБЅёцХыµгЈ¬ЅбєПєЇКэНјПуЈ¬Зу![]() µДИЎЦµ·¶О§Ј®
µДИЎЦµ·¶О§Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ЛД±ЯРОABCDКЗѕШРОЈ¬µгEФЪBC±ЯЙПЈ¬µгFФЪBCСУі¤ПЯЙПЈ¬ЗТЎПCDF =ЎПBAEЈ®
ЈЁ1Ј©ЗуЦ¤ЈєЛД±ЯРОAEFDКЗЖЅРРЛД±ЯРОЈ»
ЈЁ2Ј©ИфDF=3Ј¬DE=4Ј¬AD=5Ј¬ЗуCDµДі¤¶ИЈ®
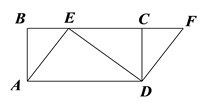
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
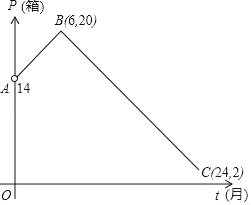
ЎѕМвДїЎїДіЦсЦЖЖ·јУ№¤і§ёщѕЭКРіЎµчСРЅб№ыЈ¬¶ФёГі§ЙъІъµДТ»ЦЦРВРНЦсЦЖЖ·НжѕЯОґАґБЅДкµДПъКЫЅшРРФ¤ІвЈ¬ІўЅЁБўИзПВДЈРНЈєЙиµЪtёцФВЈ¬ЦсЦЖЖ·ПъКЫБїОЄPЈЁµҐО»ЈєПдЈ©Ј¬PУлtЦ®јдґжФЪИзНјЛщКѕєЇКэ№ШПµЈ¬ЖдНјПуКЗПЯ¶ОABЈЁІ»є¬µгAЈ©єНПЯ¶ОBCµДЧйєПЈ®ЙиµЪtёцФВПъКЫГїПдµДГ«АыИуОЄQЈЁ°ЩФЄЈ©Ј¬ЗТQУлtВъЧгИзПВ№ШПµQ=2t+8ЈЁ0ЎЬtЎЬ24Ј©Ј®
ЈЁ1Ј©ЗуPУлtµДєЇКэ№ШПµКЅЈЁ6ЎЬtЎЬ24Ј©Ј®
ЈЁ2Ј©ёГі§ФЪµЪјёёцФВДЬ№»»сµГЧоґуГ«АыИуЈїЧоґуГ«АыИуКЗ¶аЙЩЈї
ЈЁ3Ј©ѕµчІй·ўПЦЈ¬µ±ФВГ«АыИуІ»µНУЪ40000ЗТІ»ёЯУЪ43200ФЄК±Ј¬ёГФВІъЖ·ФІДБП№©ёшєНКРіЎКЫЧоєНРіЈ¬ґЛК±іЖХвёцФВОЄЎ°єНРіФВЎ±Ј¬ДЗГґЈ¬ФЪОґАґБЅДкЦРµЪјёёцФВОЄєНРіФВЈї
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
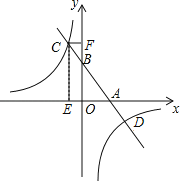
ЎѕМвДїЎїИзНјЈ¬ТСЦЄТ»ґОєЇКэyЈЅkx+bµДНјПуУлxЦбЈ¬yЦб·Ц±рПаЅ»УЪAЈ¬BБЅµгЈ¬ЗТУл·ґ±ИАэєЇКэyЈЅ![]() Ѕ»УЪµгCЈ¬DЈ®ЧчCEЎНxЦбЈ¬ґ№ЧгОЄEЈ¬CFЎНyЦбЈ¬ґ№ЧгОЄFЈ®µгBОЄOFµДЦРµгЈ¬ЛД±ЯРОOECFµДГж»эОЄ16Ј¬µгDµДЧш±кОЄЈЁ4Ј¬©ЃbЈ©Ј®
Ѕ»УЪµгCЈ¬DЈ®ЧчCEЎНxЦбЈ¬ґ№ЧгОЄEЈ¬CFЎНyЦбЈ¬ґ№ЧгОЄFЈ®µгBОЄOFµДЦРµгЈ¬ЛД±ЯРОOECFµДГж»эОЄ16Ј¬µгDµДЧш±кОЄЈЁ4Ј¬©ЃbЈ©Ј®
ЈЁ1Ј©ЗуТ»ґОєЇКэ±нґпКЅєН·ґ±ИАэєЇКэ±нґпКЅЈ»
ЈЁ2Ј©ЗуіцµгCЧш±кЈ¬ІўёщѕЭНјПуЦ±ЅУРґіцІ»µИКЅkx+bЎЬ![]() µДЅвјЇЈ®
µДЅвјЇЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїДіµкТтОЄѕУЄІ»ЙЖЗ·ПВ68400ФЄµДОЮПўґыїоµДХ®ОсЈ¬ПлЧЄРРѕУЄ·юЧ°ЧЁВфµкУЦИ±ЙЩЧКЅрЈ®Ў°ЦР№ъГОПлРгЎ±АёДїЧйѕц¶ЁЅиёшёГµк30000ФЄЧКЅрЈ¬ІўФј¶ЁАыУГѕУЄµДАыИ󳥻№Х®ОсЈЁЛщУРХ®ОсѕщІ»јЖАыПўЈ©Ј®ТСЦЄёГµкґъАнµДЖ·ЕЖ·юЧ°µДЅшјЫОЄГїјю40ФЄЈ¬ёГЖ·ЕЖ·юЧ°ИХПъКЫБї![]() ЈЁјюЈ©УлПъКЫјЫ
ЈЁјюЈ©УлПъКЫјЫ![]() ЈЁФЄјюЈ©Ц®јдµД№ШПµїЙУГНјЦРµДТ»МхХЫПЯЈЁКµПЯЈ©Аґ±нКѕЈ®ёГµкУ¦Ц§ё¶Ф±№¤µД№¤ЧКОЄГїИЛГїМм82ФЄЈ¬ГїМм»№У¦Ц§ё¶ЖдЛь·СУГОЄ106ФЄЈЁІ»°ьє¬Х®ОсЈ©Ј®
ЈЁФЄјюЈ©Ц®јдµД№ШПµїЙУГНјЦРµДТ»МхХЫПЯЈЁКµПЯЈ©Аґ±нКѕЈ®ёГµкУ¦Ц§ё¶Ф±№¤µД№¤ЧКОЄГїИЛГїМм82ФЄЈ¬ГїМм»№У¦Ц§ё¶ЖдЛь·СУГОЄ106ФЄЈЁІ»°ьє¬Х®ОсЈ©Ј®
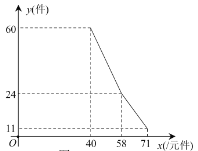
ЈЁ1Ј©ЗуИХПъКЫБї![]() ЈЁјюЈ©УлПъКЫјЫ
ЈЁјюЈ©УлПъКЫјЫ![]() ЈЁФЄ/јюЈ©Ц®јдµДєЇКэ№ШПµКЅЈ»
ЈЁФЄ/јюЈ©Ц®јдµДєЇКэ№ШПµКЅЈ»
ЈЁ2Ј©ИфёГµкФЭІ»їјВЗіҐ»№Х®ОсЈ¬µ±ДіМмµДПъКЫјЫОЄ48ФЄ/јюК±Ј¬µ±МмХэєГКХЦ§ЖЅєвЈЁКХИл=Ц§іцЈ©Ј¬ЗуёГµкФ±№¤µДИЛКэЈ»
ЈЁ3Ј©ИфёГµкЦ»УР2ГыФ±№¤Ј¬ФтёГµкЧоФзРиТЄ¶аЙЩМмДЬ»№ЗеЛщУРХ®ОсЈ¬ґЛК±Гїјю·юЧ°µДјЫёсУ¦¶ЁОЄ¶аЙЩФЄЈї
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїХэ·ЅРО![]() µД±Яі¤ОЄ
µД±Яі¤ОЄ![]() Ј¬µг
Ј¬µг![]() ·Ц±рКЗПЯ¶О
·Ц±рКЗПЯ¶О![]() ЙПµД¶ЇµгЈ¬Б¬ЅУ
ЙПµД¶ЇµгЈ¬Б¬ЅУ![]() ІўСУі¤Ј¬Ѕ»±Я
ІўСУі¤Ј¬Ѕ»±Я![]() УЪ
УЪ![]() Ј¬№э
Ј¬№э![]() Чч
Чч![]() Ј¬ґ№ЧгОЄ
Ј¬ґ№ЧгОЄ![]() Ј¬Ѕ»±Я
Ј¬Ѕ»±Я![]() УЪµг
УЪµг![]() Ј®
Ј®
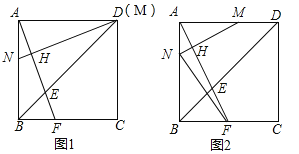
ЈЁ1Ј©ИзНј1Ј¬Ифµг![]() Улµг
Улµг![]() ЦШєПЈ¬ЗуЦ¤Јє
ЦШєПЈ¬ЗуЦ¤Јє![]() Ј»
Ј»
ЈЁ2Ј©ИзНј2Ј¬Ифµг![]() ґУµг
ґУµг![]() іц·ўЈ¬ТФ
іц·ўЈ¬ТФ![]() µДЛЩ¶ИСШ
µДЛЩ¶ИСШ![]() Птµг
Птµг![]() ФЛ¶ЇЈ¬Н¬К±µг
ФЛ¶ЇЈ¬Н¬К±µг![]() ґУµг
ґУµг![]() іц·ўЈ¬ТФ
іц·ўЈ¬ТФ![]() µДЛЩ¶ИСШ
µДЛЩ¶ИСШ![]() Птµг
Птµг![]() ФЛ¶ЇЈ¬ФЛ¶ЇК±јдОЄ
ФЛ¶ЇЈ¬ФЛ¶ЇК±јдОЄ![]() Ј®
Ј®
ўЩЙи![]() ,Зу
,Зу![]() №ШУЪ
№ШУЪ![]() µДєЇКэ±нґпКЅЈ»
µДєЇКэ±нґпКЅЈ»
ўЪµ±![]() К±Ј¬Б¬ЅУ
К±Ј¬Б¬ЅУ![]() Ј¬Зу
Ј¬Зу![]() µДі¤Ј®
µДі¤Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪЖЅГжЦ±ЅЗЧш±кПµЦРЈ¬Хэ·ЅРОOABCµД±Яі¤ОЄ4Ј¬°СЛьДЪІїј°±ЯЙПµДєбЎўЧЭЧш±кѕщОЄХыКэµДµгіЖОЄХыµгЈ¬µгPОЄЕЧОпПЯ![]() µД¶ҐµгЈЁmОЄХыКэЈ©Ј¬µ±µгPФЪХэ·ЅРОOABCДЪІї»т±ЯЙПК±Ј¬ЕЧОпПЯПВ·ЅЈЁ°ьАЁ±ЯЅзЈ©µДХыµгЧоЙЩУРЈЁЎЎЎЎЈ©
µД¶ҐµгЈЁmОЄХыКэЈ©Ј¬µ±µгPФЪХэ·ЅРОOABCДЪІї»т±ЯЙПК±Ј¬ЕЧОпПЯПВ·ЅЈЁ°ьАЁ±ЯЅзЈ©µДХыµгЧоЙЩУРЈЁЎЎЎЎЈ©
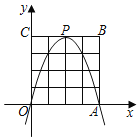
A.3ёцB.5ёцC.10ёцD.15ёц
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬Ѕ«ХэБщ±ЯРОABCDEF·ЕЦГФЪЦ±ЅЗЧш±кПµДЪЈ¬A(©Ѓ2Ј¬0)Ј¬µгBФЪФµгЈ¬°СХэБщ±ЯРОABCDEFСШxЦбХэ°лЦбЧчОЮ»¬¶ЇµДБ¬Рш·ЧЄЈ¬ГїґО·ЧЄ60ЎгЈ¬ѕ№э2020ґО·ЧЄЦ®єуЈ¬µгCµДЧш±кКЗ_____Ј®
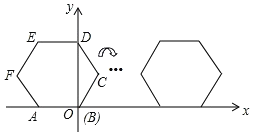
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com