
【题目】如图,四边形ABCD是矩形,点E在BC边上,点F在BC延长线上,且∠CDF =∠BAE.
(1)求证:四边形AEFD是平行四边形;
(2)若DF=3,DE=4,AD=5,求CD的长度.
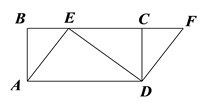
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
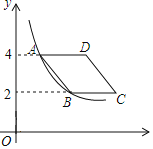
【题目】如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为4,2,反比例函数y![]() (x>0)的图象经过A,B两点,若菱形ABCD的面积为2
(x>0)的图象经过A,B两点,若菱形ABCD的面积为2![]() ,则k的值为( )
,则k的值为( )
A. 2B. 3C. 4D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
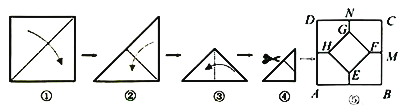
【题目】将一张正方形纸片按如图步骤,通过折叠得到图④,再沿虚线剪去一个角,展开铺平后得到图⑤,其中![]() 是折痕.若正方形
是折痕.若正方形![]() 与五边形
与五边形![]() 的面积相等,则
的面积相等,则![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+(2m﹣1)x﹣2m(m>0.5)的最低点的纵坐标为﹣4.
(1)求抛物线的解析式;
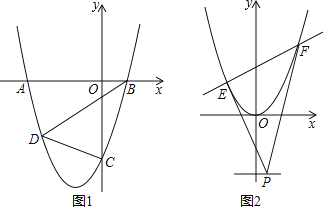
(2)如图1,抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,D为抛物线上的一点,BD平分四边形ABCD的面积,求点D的坐标;
(3)如图2,平移抛物线y=x2+(2m﹣1)x﹣2m,使其顶点为坐标原点,直线y=﹣2上有一动点P,过点P作两条直线,分别与抛物线有唯一的公共点E、F(直线PE、PF不与y轴平行),求证:直线EF恒过某一定点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在国家大数据战略的引领下,我国在人工智能领域取得显著成就,自主研发的人工智能“绝艺”获得全球最前沿的人工智能赛事冠军,这得益于所建立的大数据中心的规模和数据存储量,它们决定着人工智能深度学习的质量和速度,其中的一个大数据中心能存储580亿本书籍,将580亿用科学记数法表示应为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
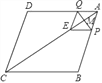
【题目】如图,在菱形ABCD中,AB=10,AC=16,点M是对角线AC上的一个动点,过点M作PQ⊥AC交AB于点P,交AD于点Q,将△APQ沿PQ折叠,点A落在点E处,当△BCE是等腰三角形时,AP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
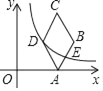
【题目】如图,菱形ABCD的顶点A在x轴的正半轴上,∠C=60°,顶点B,D的纵坐标相同,已知点B的横坐标为7![]() ,若过点D的双曲线y=
,若过点D的双曲线y=![]() (k>0)恰好过边AB的中点E,则k=_____.
(k>0)恰好过边AB的中点E,则k=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线![]() 与抛物线
与抛物线![]() 的形状相同,开口方向相反,且相交于点
的形状相同,开口方向相反,且相交于点![]() 和点
和点![]() .抛物线
.抛物线![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() 为抛物线
为抛物线![]() 上
上![]() 两点间一动点,过点
两点间一动点,过点![]() 作直线
作直线![]() 轴,与
轴,与![]() 交于点
交于点![]() .
.
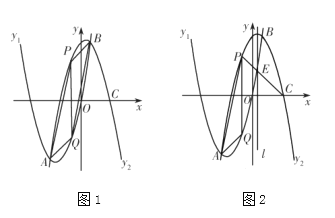
(1)求抛物线![]() 与抛物线
与抛物线![]() 的解析式;
的解析式;
(2)四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值,并写出此时点
的最大值,并写出此时点![]() 的坐标;
的坐标;
(3)如图2,![]() 的对称轴为直线
的对称轴为直线![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,在(2)的条件下,直线
,在(2)的条件下,直线![]() 上是否存在一点
上是否存在一点![]() ,使得以
,使得以![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?如果存在,求出点
相似?如果存在,求出点![]() 的坐标;如果不存在,说明理由.
的坐标;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CE是⊙O的直径,BD切⊙O于点D,DE∥BO,CE的延长线交BD于点A.
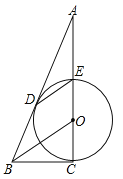
(1)求证:直线BC是⊙O的切线;
(2)若AE=2,tan∠DEO=![]() ,求AO的长.
,求AO的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com