
����Ŀ����֪������y��x2+��2m��1��x��2m��m��0.5������͵��������Ϊ��4��
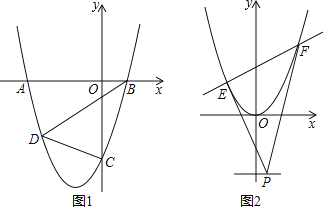
��1���������ߵĽ���ʽ��
��2����ͼ1����������x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��DΪ�������ϵ�һ�㣬BDƽ���ı���ABCD����������D�����ꣻ
��3����ͼ2��ƽ��������y��x2+��2m��1��x��2m��ʹ�䶥��Ϊ����ԭ�㣬ֱ��y����2����һ����P������P������ֱ�ߣ��ֱ�����������Ψһ�Ĺ�����E��F��ֱ��PE��PF����y��ƽ�У�����֤��ֱ��EF���ijһ���㣮
���𰸡���1��y��x2+2x��3����2��D����![]() ����
����![]() ������3��������
������3��������
��������
��1��������������꣬����͵��������Ϊ��4�����з��̣�������⣻
��2����AC��BD��E����A��AM��BD��M����C��CN��BD��N���������������ϵ��ȫ�������ε����ʿ����E���꣬����BD����ʽ���������D���ꣻ
��3����E��t��t2����F��n��n2��������PE����ʽ��������������Ψһ�Ĺ����㣬����k1��2t���������P�����꣬�ɵ�tn����2����ֱ��EF�Ľ���ʽΪy��kx+b����x2��kx��b��0������b��2�����ɵ�ֱ��EF������㣨0��2����
�⣺��1����y��x2+��2m��1��x��2m����x+m��0.5��2��m2��m��0.25��
�ඥ������Ϊ��0.5��m����m2��m��0.25��
����͵��������Ϊ��4��
�ੁm2��m��0.25����4����4m2+4m��15��0��
��m��1.5��2.5��
��m��0.5����m��1.5��
�������ߵĽ���ʽΪy��x2+2x��3��
��2����y��x2+2x��3��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��
��A����3��0����B��1��0����C��0����3����
��ͼ����AC��BD��E����A��AM��BD��M����C��CN��BD��N��
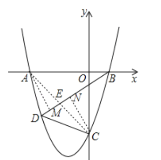
��BDƽ���ı���ABCD�������
��S��ABD��S��CBD��
��![]() BD��AM��
BD��AM��![]() BD��CN��
BD��CN��
��AM��CN���ҡ�AEM����CMN����AME����CNE��90��
���AEM�ա�CEN��AAS����
��AE��CE��
��E����1.5����1.5������B��1��0����
��ֱ��BE�Ľ���ʽΪy��0.6x��0.6��
��0.6x��0.6��x2+2x��3��
���x1����![]() ��x2��1��
��x2��1��
��D����![]() ����
����![]() ����
����
��3��������ɵ�ƽ�ƺ����ʽΪy��x2��
��E��t��t2����F��n��n2����
��ֱ��PEΪy��k1��x��t��+t2��
������ɵ� x2��k1x+k1t��t2��0��
�����k12��4��k1t��t2������k1��2t��2��0��
��k1��2t��
��ֱ��PEΪy��2t��x��t��+t2����y��2tx��t2��
��y����2����xP��![]() ��
��
ͬ������ֱ��PFΪy��k2��x��n��+n2��
��xP��![]() ��
��
��![]() ��
��![]() ��
��
��t��n��
��tn����2��
��ֱ��EF�Ľ���ʽΪy��kx+b����x2��kx��b��0��
��xExF����b����tn����b��
��b��2��
��ֱ��EFΪy��kx+2�������㣨0��2����


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���ֱ��������![]() �У�
��![]() ����
����![]() Ϊ
Ϊ![]() �е㣬��
�е㣬��![]() Ϊ��
Ϊ��![]() һ�㣬��֪
һ�㣬��֪![]() ����CD�ij�Ϊ�� ����
����CD�ij��� ����

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ������
������![]() ����ƽ��������λ���ȣ��õ���
����ƽ��������λ���ȣ��õ���![]() ����
����![]() ���������ϣ�
���������ϣ�
��1����ֱ��д�������ߵĶԳ�����__________��
���ú�![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() ��
��
��2���ᡢ�����궼�������ĵ�������㣮��![]() ǡ��Ϊ���㣬���������ڵ�
ǡ��Ϊ���㣬���������ڵ�![]() ��
��![]() ֮��IJ������߶�
֮��IJ������߶�![]() ��Χ�ɵ������ڣ������߽磩ǡ���������㣬��Ϻ���ͼ����
��Χ�ɵ������ڣ������߽磩ǡ���������㣬��Ϻ���ͼ����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB��AC��AO��BC�ڵ�O��OE��AB�ڵ�E���Ե�OΪԲ�ģ�OEΪ�뾶����Բ����AO�ڵ�F��
��1����֤��AC����O�����ߣ�
��2������F��OA���е㣬OE��3����ͼ����Ӱ���ֵ������
��3���ڣ�2���������£���P��BC���ϵĶ��㣬��PE+PFȡ��Сֵʱ��ֱ��д��BP�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ�п�չ�������������˶����Ļ���Թ���ѧ��������������������Ϊ�˽�ѧ��ÿ����������ʱ�䣬ѧУ�ڻ֮ǰ���꼶ͬѧ�����˳������ˣ������ݵ��˽����ѧ��ÿ�ܵ���������ʱ���Ϊ3Сʱ��4Сʱ��5Сʱ��6Сʱ��7Сʱ�����������С�����ݵ���ṹ��������ͼ����ͳ��ͼ��������ͼ��������Ϣ����������⣺
���������ݣ�
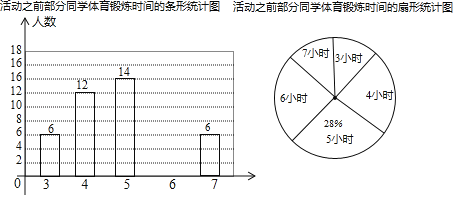
�����������˶����Ļ����֮���ٴγ���ⲿ��ѧ������������ʱ�䣺
һ����������ʱ�䣨Сʱ�� | 3 | 4 | 5 | 6 | 7 |
���� | 3 | 5 | 15 | a | 10 |
�֮��ѧ����������ʱ���ͳ�Ʊ�
���������ݣ�
ƽ���� | ��λ�� | ���� | |
�֮ǰ����ʱ�䣨Сʱ�� | 5 | 5 | 5 |
�֮�����ʱ�䣨Сʱ�� | 5.52 | b | c |
����ݵ�����Ϣ
��1����ȫ����ͳ��ͼ��������a���� ����b���� ��Сʱ��c���� ��Сʱ��
��2��С��ͬѧ�ڻ֮ǰ��֮��������ε����У���������ʱ���Ϊ5Сʱ��������������ʱ���ɶൽ�ٽ�������ͳ�ƣ��������ڱ�����ͬѧ����������ʱ��������ǰ������ ������֮ǰ���֮������������ ����
��3����֪���꼶��2200��ѧ���������ȫ�꼶ѧ���ڻ������ÿ����������ʱ��������6Сʱ��ѧ�������ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����C�ǡ�O��һ�㣬D��![]() ���е㣬EΪOD�ӳ�����һ�㣬�ҡ�CAE��2��C��AC��BD���ڵ�H����OE���ڵ�F��
���е㣬EΪOD�ӳ�����һ�㣬�ҡ�CAE��2��C��AC��BD���ڵ�H����OE���ڵ�F��
��1����֤��AE�ǡ�O�����ߣ�
��2����DH��9��tanC��![]() ����ֱ��AB�ij���
����ֱ��AB�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�Ǿ��Σ���E��BC���ϣ���F��BC�ӳ����ϣ��ҡ�CDF =��BAE��
��1����֤���ı���AEFD��ƽ���ı��Σ�
��2����DF=3��DE=4��AD=5����CD�ij��ȣ�
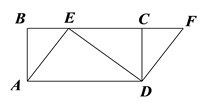
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
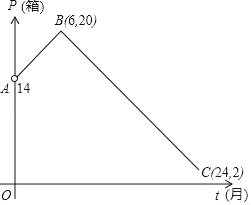
����Ŀ��ij����Ʒ�ӹ��������г����н�����Ըó�������һ����������Ʒ���δ����������۽���Ԥ�⣬����������ģ�ͣ����t���£�����Ʒ������ΪP����λ���䣩��P��t֮�������ͼ��ʾ������ϵ����ͼ�����߶�AB��������A�����߶�BC����ϣ����t��������ÿ���ë����ΪQ����Ԫ������Q��t�������¹�ϵQ=2t+8��0��t��24����
��1����P��t�ĺ�����ϵʽ��6��t��24����
��2���ó��ڵڼ������ܹ�������ë�������ë�����Ƕ��٣�
��3�������鷢�֣�����ë������40000�Ҳ�����43200Ԫʱ�����²�Ʒԭ���Ϲ������г������г����ʱ�������Ϊ����г��������ô����δ�������еڼ�����Ϊ��г�£�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������OABC�ı߳�Ϊ4�������ڲ������ϵĺᡢ�������Ϊ�����ĵ��Ϊ���㣬��PΪ������![]() �Ķ��㣨mΪ������������P��������OABC�ڲ������ʱ���������·��������߽磩�����������У�������
�Ķ��㣨mΪ������������P��������OABC�ڲ������ʱ���������·��������߽磩�����������У�������
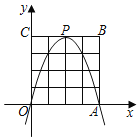
A.3��B.5��C.10��D.15��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com