
����Ŀ������һ�п�չ�������������˶����Ļ���Թ���ѧ��������������������Ϊ�˽�ѧ��ÿ����������ʱ�䣬ѧУ�ڻ֮ǰ���꼶ͬѧ�����˳������ˣ������ݵ��˽����ѧ��ÿ�ܵ���������ʱ���Ϊ3Сʱ��4Сʱ��5Сʱ��6Сʱ��7Сʱ�����������С�����ݵ���ṹ��������ͼ����ͳ��ͼ��������ͼ��������Ϣ����������⣺
���������ݣ�
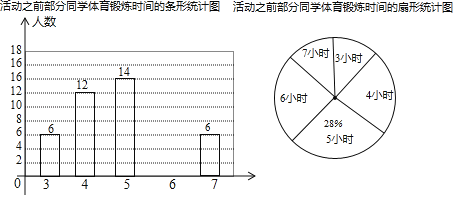
�����������˶����Ļ����֮���ٴγ���ⲿ��ѧ������������ʱ�䣺
һ����������ʱ�䣨Сʱ�� | 3 | 4 | 5 | 6 | 7 |
���� | 3 | 5 | 15 | a | 10 |
�֮��ѧ����������ʱ���ͳ�Ʊ�
���������ݣ�
ƽ���� | ��λ�� | ���� | |
�֮ǰ����ʱ�䣨Сʱ�� | 5 | 5 | 5 |
�֮�����ʱ�䣨Сʱ�� | 5.52 | b | c |
����ݵ�����Ϣ
��1����ȫ����ͳ��ͼ��������a���� ����b���� ��Сʱ��c���� ��Сʱ��
��2��С��ͬѧ�ڻ֮ǰ��֮��������ε����У���������ʱ���Ϊ5Сʱ��������������ʱ���ɶൽ�ٽ�������ͳ�ƣ��������ڱ�����ͬѧ����������ʱ��������ǰ������ ������֮ǰ���֮������������ ����
��3����֪���꼶��2200��ѧ���������ȫ�꼶ѧ���ڻ������ÿ����������ʱ��������6Сʱ��ѧ�������ж����ˣ�
���𰸡�(1) 17��6��6��(2) �֮ǰ���֮ǰС������������ʱ�䲢������19�������֮����������28����(3) ���꼶2200��ѧ���У����ڻ������ÿ����������ʱ��������6Сʱ��ѧ����Լ��1188�ˣ�
��������
��1������������5Сʱ������14�ˣ�ռ����������28%������������������ٸ��ݻ������ѧ����������ʱ�䡱��ͳ�Ʊ��������a��ֵ����������������������ʱ�����λ����������ȷ��b��c��ֵ��
��2���õ�����������ʱ��5Сʱ���ڻǰ���������������ɵó����ۣ�
��3�������������壬�����С�ÿ����������ʱ������6Сʱ��ռ����������![]() ����������2200�˵�
����������2200�˵�![]() �ǡ�ÿ����������ʱ������6Сʱ����������
�ǡ�ÿ����������ʱ������6Сʱ����������
�⣺��1�������������Ϊ��14��28%��50���ˣ���a��50��3��5��10��15��17���ˣ���
��������ٳ�飬��������ʱ��������6Сʱ����17�ˣ����������6Сʱ��
����������ʱ���С�������к��ڵ�25λ��26λ������������6Сʱ�������λ����6��
�ʴ�Ϊ��17��6��6��
��2���֮ǰ����������Ϊ6Сʱ���У�50��6��12��14��6��12�ˣ�С��5Сʱ����ʱ��IJ�������Ϊ��12+6+1��19����
���֮��С��5Сʱ����ʱ��IJ�������Ϊ��17+10+1��28����
�ʴ�Ϊ���֮ǰ���֮ǰС������������ʱ�䲢������19�������֮����������28��
��3��2200��![]() ��1188���ˣ���
��1188���ˣ���
�𣺰��꼶2200��ѧ���У����ڻ������ÿ����������ʱ��������6Сʱ��ѧ����Լ��1188�ˣ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�ڼ䣬�ס��������ڸ����ľ������棬�״�![]() ��������������ѡ��һ�����棬�Ҵ�
��������������ѡ��һ�����棬�Ҵ�![]() ��������������ѡ��һ�����森
��������������ѡ��һ�����森
��1����ǡ������![]() ����ĸ���Ϊ����������
����ĸ���Ϊ����������
��2�����б�����״ͼ�ķ����г��ס���ǡ������ͬһ��������еȿ��ܵĽ��������ס���ǡ������ͬһ����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���![]() �У�
�У�![]() Ϊһ���Խ��ߣ�
Ϊһ���Խ��ߣ�![]() ��
��![]() ��
��![]() ��
��![]() Ϊ
Ϊ![]() ���е㣬����
���е㣬����![]() ��
��
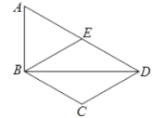
��1����֤���ı���![]() Ϊ���Σ�
����
��2������![]() ����
����![]() ƽ��
ƽ��![]() ��
��![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
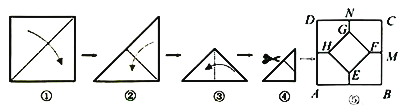
����Ŀ����һ��������ֽƬ����ͼ���裬ͨ���۵��õ�ͼ�ܣ���������ȥһ���ǣ�չ����ƽ��õ�ͼ�ݣ�����![]() ���ۺۣ���������
���ۺۣ���������![]() �������
�������![]() �������ȣ���
�������ȣ���![]() ��ֵ�ǣ� ��
��ֵ�ǣ� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ⱳ��������ѧϰ�ȱ�������ʱ�õ�ֱ�������ε�һ�����ʣ���ֱ���������У����һ����ǵ���30������ô�����Ե�ֱ�DZߵ���б�ߵ�һ�룮������ͼ1����Rt��ABC�У���ACB=90�㣬��ABC=30�㣬��AC=![]() AB��
AB��

̽�����ۣ�С��ͬѧ�����Ͻ������˽�һ���о���
��1����ͼ1������AB��������CE������CE=![]() AB���ý��ۣ��١�ACEΪ�ȱ������Σ���BE��CE֮���������ϵΪ������
AB���ý��ۣ��١�ACEΪ�ȱ������Σ���BE��CE֮���������ϵΪ������
��2����ͼ2����D�DZ�CB������һ�㣬����AD�����ȱ���ADE���ҵ�E�ڡ�ACB���ڲ�������BE����̽���߶�BE��DE֮���������ϵ��д����IJ��벢����֤����
��3������DΪ��CB�ӳ���������һ��ʱ���ڣ�2�������Ļ����ϣ��߶�BE��DE֮�����������������ϵ����ֱ��д����Ľ���������
��չӦ�ã���ͼ3����ƽ��ֱ������ϵxOy�У���A������Ϊ����![]() ��1������B��x���������ϵ�һ���㣬��ABΪ�����ȱ���ABC����C���ڵ�һ�����ڣ���B��2��0��ʱ����C������꣮
��1������B��x���������ϵ�һ���㣬��ABΪ�����ȱ���ABC����C���ڵ�һ�����ڣ���B��2��0��ʱ����C������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
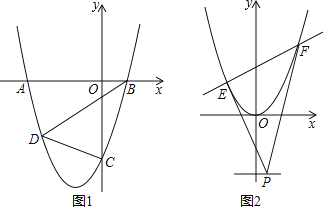
����Ŀ����֪������y��x2+��2m��1��x��2m��m��0.5������͵��������Ϊ��4��
��1���������ߵĽ���ʽ��
��2����ͼ1����������x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��DΪ�������ϵ�һ�㣬BDƽ���ı���ABCD����������D�����ꣻ
��3����ͼ2��ƽ��������y��x2+��2m��1��x��2m��ʹ�䶥��Ϊ����ԭ�㣬ֱ��y����2����һ����P������P������ֱ�ߣ��ֱ�����������Ψһ�Ĺ�����E��F��ֱ��PE��PF����y��ƽ�У�����֤��ֱ��EF���ijһ���㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڹ��Ҵ�����ս�Ե������£��ҹ����˹���������ȡ�������ɾͣ������з����˹����ܡ����ա����ȫ����ǰ�ص��˹��������¹ھ�����������������Ĵ��������ĵĹ�ģ�����ݴ洢�������Ǿ������˹��������ѧϰ���������ٶȣ����е�һ�������������ܴ洢580�ڱ��鼮����580���ÿ�ѧ��������ʾӦΪ�� ����
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
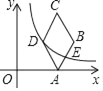
����Ŀ����ͼ������ABCD�Ķ���A��x����������ϣ���C��60�㣬����B��D����������ͬ����֪��B�ĺ�����Ϊ7![]() ��������D��˫����y��
��������D��˫����y��![]() ��k��0��ǡ�ù���AB���е�E����k��_____��
��k��0��ǡ�ù���AB���е�E����k��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ������B��3��0����C��0��-2����ֱ��L��
������B��3��0����C��0��-2����ֱ��L��![]() ��y���ڵ�E�����������߽���A��D���㣬PΪ��������һ���㣨����A�غϣ���
��y���ڵ�E�����������߽���A��D���㣬PΪ��������һ���㣨����A�غϣ���
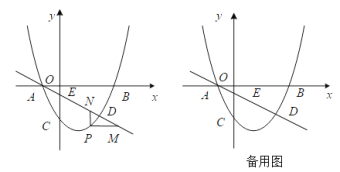
��1���������ߵĽ���ʽ��
��2������P��ֱ��L�·�ʱ������P��PM��x�ύL�ڵ�M��PN��y�ύL�ڵ�N����PM+PN�����ֵ��
��3����FΪֱ��L�ϵĵ㣬��E��C��P��FΪ������ı����ܷ�ƽ���ı��Σ����ܣ������F�����ꣻ�����ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com