
【题目】如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为4,2,反比例函数y![]() (x>0)的图象经过A,B两点,若菱形ABCD的面积为2
(x>0)的图象经过A,B两点,若菱形ABCD的面积为2![]() ,则k的值为( )
,则k的值为( )
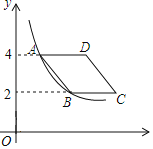
A. 2B. 3C. 4D. 6
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是垂直于水平面的建筑物.为测量AB的高度,小红从建筑物底端B点出发,沿水平方向行走了52米到达点C,然后沿斜坡CD前进,到达坡顶D点处,![]() .在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角
.在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角![]() 为
为![]() (点A,B,C,D,E在同一平面内).斜坡CD的坡度(或坡比)
(点A,B,C,D,E在同一平面内).斜坡CD的坡度(或坡比)![]() ,那么建筑物AB的高度约为( )
,那么建筑物AB的高度约为( )
(参考数据![]() ,
,![]() ,
,![]() )
)
A.65.8米B.71.8米C.73.8米D.119.8米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数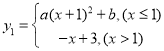 (
(![]() 为常数且
为常数且![]() ),已知当
),已知当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,请对该函数及其图像进行如下探究:
,请对该函数及其图像进行如下探究:

(1)求函数![]() 的解析式;
的解析式;
(2)如图,请在平面直角坐标系中,画出该函数的图像;
(3)结合所画函数图像,请写出该函数的一条性质;
(4)解决问题:若函数![]() 与
与![]() 至少有两个公共点,请直接写出
至少有两个公共点,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是![]() 的中点,连接AC并延长至点D,使CD=AC,点E是OB上一点,且
的中点,连接AC并延长至点D,使CD=AC,点E是OB上一点,且![]() ,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.
,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.

(1)求证:BD是⊙O的切线;(2)当OB=2时,求BH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
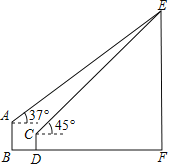
【题目】如图,甲楼AB高20米,乙楼CD高10米,两栋楼之间的水平距离BD=30m,为了测量某电视塔EF的高度,小明在甲楼楼顶A处观测电视塔塔顶E,测得仰角为37°,小明在乙楼楼顶C处观测电视塔塔顶E,测得仰角为45°,求该电视塔的高度EF.
(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 与
与![]() 轴交于点
轴交于点![]() ,将点
,将点![]() 向右平移两个单位长度,得到点
向右平移两个单位长度,得到点![]() ,点
,点![]() 在抛物线上.
在抛物线上.
(1)①直接写出抛物线的对称轴是__________;
②用含![]() 的代数式表示
的代数式表示![]() ;
;
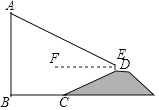
(2)横、纵坐标都是整数的点叫做整点.点![]() 恰好为整点,若抛物线在点
恰好为整点,若抛物线在点![]() 、
、![]() 之间的部分与线段
之间的部分与线段![]() 所围成的区域内(不含边界)恰有两个整点,结合函数图象,求
所围成的区域内(不含边界)恰有两个整点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,点E在BC边上,点F在BC延长线上,且∠CDF =∠BAE.
(1)求证:四边形AEFD是平行四边形;
(2)若DF=3,DE=4,AD=5,求CD的长度.
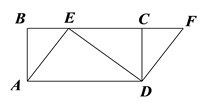
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com