
【题目】已知函数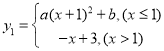 (
(![]() 为常数且
为常数且![]() ),已知当
),已知当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,请对该函数及其图像进行如下探究:
,请对该函数及其图像进行如下探究:

(1)求函数![]() 的解析式;
的解析式;
(2)如图,请在平面直角坐标系中,画出该函数的图像;
(3)结合所画函数图像,请写出该函数的一条性质;
(4)解决问题:若函数![]() 与
与![]() 至少有两个公共点,请直接写出
至少有两个公共点,请直接写出![]() 的取值范围.
的取值范围.
【答案】(1)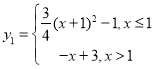 ;(2)画出该函数的图像见解析;(3)当
;(2)画出该函数的图像见解析;(3)当![]() 时,
时,![]() 随
随![]() 的增大而减小;(4)
的增大而减小;(4)![]() .
.
【解析】
(1)将![]() ,
,![]() ;
;![]() ,
,![]() 代入函数解析式列出方程组求解即可;
代入函数解析式列出方程组求解即可;
(2)利用函数解析式分别求出对应的函数值即可,利用描点法画出图象即可;
(3)观察图象可知:当x>1时,y随x的增大而减小;
(4)利用图象即可解决问题.
解:(1)将![]() ,
,![]() ;
;![]() ,
,![]() 代入函数解析式
代入函数解析式![]()
得:![]()
解得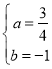
∴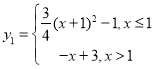
(2)列表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | …… |
y | … | 2 |
| ﹣1 |
| 2 | 1 | 0 | ﹣1 | …… |
描点,连线:

(3)答:观察图象可知:当![]() 时,
时,![]() 随
随![]() 的增大而减小
的增大而减小
(4)由图像可知,当直线![]() 经过点(1,2)时,此时函数
经过点(1,2)时,此时函数![]() 与
与![]() 有两个公共点,
有两个公共点,
则2=2t-2,t=2,
当直线![]() 经过点(﹣1,﹣1)时,此时函数
经过点(﹣1,﹣1)时,此时函数![]() 与
与![]() 有两个公共点,
有两个公共点,
则﹣1=2t-2,t=![]() ,
,
∵函数![]() 与
与![]() 至少有两个公共点,
至少有两个公共点,
∴由图像可知,t的取值范围是:![]()


 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
【题目】[知识回顾]
七年级学习代数式求值时,遇到这样一类题 “代数式![]() 的值与
的值与![]() 的取值无关,求
的取值无关,求![]() 的值”,通常的解题方法是:把
的值”,通常的解题方法是:把![]() 看作字母,
看作字母,![]() 看作系数合并同类项,因为代数式的值与
看作系数合并同类项,因为代数式的值与![]() 的取值无关,所以含
的取值无关,所以含![]() 项的系数为
项的系数为![]() ,即原式
,即原式![]() ,所以
,所以![]() ,则
,则![]() .
.
[理解应用]
![]() 若关于
若关于![]() 的多项式
的多项式![]() 的值与
的值与![]() 的取值无关,试求
的取值无关,试求![]() 的值:
的值:
![]() 若一次函数
若一次函数![]() 的图像经过某个定点,则该定点坐标为 ;
的图像经过某个定点,则该定点坐标为 ;
[能力提升]
![]() 张如图1的小长方形,长为
张如图1的小长方形,长为![]() ,宽为
,宽为![]() ,按照图2方式不重叠地放在大矩形
,按照图2方式不重叠地放在大矩形![]() 内,大矩形中未被覆盖的两个部分(图中阴影部分) ,设右上角的面积为
内,大矩形中未被覆盖的两个部分(图中阴影部分) ,设右上角的面积为![]() ,左下角的面积为
,左下角的面积为![]() ,当
,当![]() 的长变化时,
的长变化时,![]() 的值始终保持不变,求
的值始终保持不变,求![]() 与
与![]() 的等量关系.
的等量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在新中国成立70周年之际,某校开展了“校园文化艺术”活动,活动项目有:书法、绘画、声乐和器乐,要求全校学生人人参加,并且每人只能参加其中一项活动,政教处在该校学生中随机抽取了100名学生进行调查和统计,并绘制了如下两幅不完整的统计图,请结合图中相关数据解答下列问题:
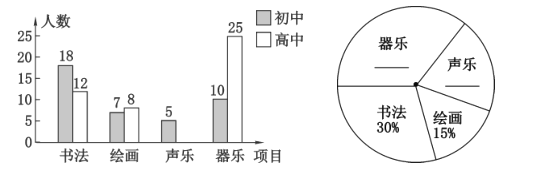
(1)请补全条形统计图和扇形统计图;
(2)该校初中学生中,参加“书法”项目的学生所占的百分比是多少?
(3)若该校共有1500人,请估计其中参加“器乐”项目的高中学生有多少人?
(4)经政教处对所有参加“绘画”项目的作品进行评比,共选出2名初中学生和2名高中学生的最佳作品,学校决定从这4名学生中随机抽取2人作为学生会“绘画社团”的团生,那么正好抽到一名初中学生和一名高中学生的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一期间,甲、乙两人在附近的景点游玩,甲从![]() 两个景点中任意选择一个游玩,乙从
两个景点中任意选择一个游玩,乙从![]() 三个景点中任意选择一个游玩.
三个景点中任意选择一个游玩.
(1)乙恰好游玩![]() 景点的概率为 .
景点的概率为 .
(2)用列表或画树状图的方法列出甲、乙恰好游玩同一景点的所有等可能的结果.并求甲、乙恰好游玩同一景点的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为4,2,反比例函数y![]() (x>0)的图象经过A,B两点,若菱形ABCD的面积为2
(x>0)的图象经过A,B两点,若菱形ABCD的面积为2![]() ,则k的值为( )
,则k的值为( )
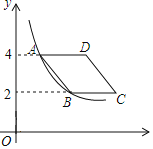
A. 2B. 3C. 4D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(1)班全体学生2018年初中毕业体育学业考试成绩统计表如下:
成绩/分 | 45 | 49 | 52 | 54 | 55 | 58 | 60 |
人数 | 2 | 5 | 6 | 6 | 8 | 7 | 6 |
根据上表中信息判断,下列结论中错误的是( )
A.该班一共有40名同学
B.该班学生这次考试成绩的众数是55分
C.该班学生这次考试成绩的中位数是55分
D.该班学生这次考试成绩的平均数是55分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在国家大数据战略的引领下,我国在人工智能领域取得显著成就,自主研发的人工智能“绝艺”获得全球最前沿的人工智能赛事冠军,这得益于所建立的大数据中心的规模和数据存储量,它们决定着人工智能深度学习的质量和速度,其中的一个大数据中心能存储580亿本书籍,将580亿用科学记数法表示应为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com