
����Ŀ��[֪ʶ�ع�]
���꼶ѧϰ����ʽ��ֵʱ����������һ���� ������ʽ![]() ��ֵ��
��ֵ��![]() ��ȡֵ�أ���
��ȡֵ�أ���![]() ��ֵ����ͨ���Ľ��ⷽ���ǣ���
��ֵ����ͨ���Ľ��ⷽ���ǣ���![]() ������ĸ��
������ĸ��![]() ����ϵ���ϲ�ͬ�����Ϊ����ʽ��ֵ��
����ϵ���ϲ�ͬ�����Ϊ����ʽ��ֵ��![]() ��ȡֵ�أ����Ժ�
��ȡֵ�أ����Ժ�![]() ���ϵ��Ϊ
���ϵ��Ϊ![]() ����ԭʽ
����ԭʽ![]() ������
������![]() ����
����![]() ��
��
[����Ӧ��]
![]() ������
������![]() �Ķ���ʽ
�Ķ���ʽ![]() ��ֵ��
��ֵ��![]() ��ȡֵ�أ�����
��ȡֵ�أ�����![]() ��ֵ��
��ֵ��
![]() ��һ�κ���
��һ�κ���![]() ��ͼ��ij�����㣬��ö�������Ϊ ��
��ͼ��ij�����㣬��ö�������Ϊ ��
[��������]
![]() ����ͼ1��С�����Σ���Ϊ
����ͼ1��С�����Σ���Ϊ![]() ����Ϊ
����Ϊ![]() ������ͼ2��ʽ���ص��ط��ڴ����
������ͼ2��ʽ���ص��ط��ڴ����![]() �ڣ��������δ�����ǵ���������(ͼ����Ӱ����) �������Ͻǵ����Ϊ
�ڣ��������δ�����ǵ���������(ͼ����Ӱ����) �������Ͻǵ����Ϊ![]() �����½ǵ����Ϊ
�����½ǵ����Ϊ![]() ����
����![]() �ij��仯ʱ��
�ij��仯ʱ��![]() ��ֵʼ�ձ��ֲ��䣬��
��ֵʼ�ձ��ֲ��䣬��![]() ��
��![]() �ĵ�����ϵ��
�ĵ�����ϵ��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
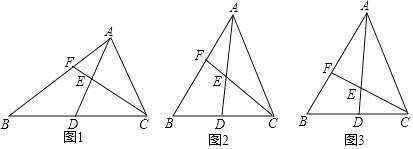
����Ŀ���ڡ�ABC�У�ADΪBC���ϵ����ߣ�EΪAD��һ���㣬��DE��nEA������CE���ӳ�����AB�ڵ�F��
��1������̽������ͼ1������BAC��90������B��30����DE��EAʱ��BF��BA֮���������ϵ���� ����
��2��������죺��ͼ2������ABCΪ��������Σ�DE��EAʱ����1���еĽ����Ƿ���Ȼ�������������������֤����������������˵�����ɣ�
��3����չǨ�ƣ���ͼ3������ABCΪ��������Σ�DE��nEAʱ����ֱ��д��BF��BA֮���������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC����CDE���ǵ��������Σ���BAC����EDC��120����
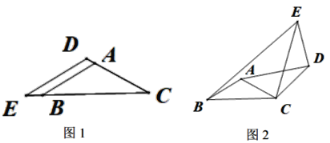
��1����ͼ1��A��D��C��ͬһֱ����ʱ��![]() ��_______��
��_______��![]() ��_______��
��_______��
��2����ͼ1�Ļ����ϣ��̶���ABC������CDE��C��תһ���ĽǶ���(0��������360��)����ͼ2������AD��BE��
�� ![]() ��ֵ��û�иı䣿��˵�����ɣ�
��ֵ��û�иı䣿��˵�����ɣ�
����չ�о�����AB��1��DE��![]() ���� B��D��E��ͬһֱ����ʱ��������߶�AD�ij���
���� B��D��E��ͬһֱ����ʱ��������߶�AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
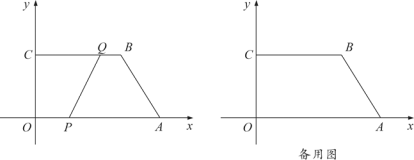
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��ı���OABC�Ķ�������ֱ�ΪO��0��0����A��6��0����B��4��3����C��0��3��������P�ӵ�O��������ÿ��![]() ����λ���ȵ��ٶ��ر�OA���յ�A�˶�������Q�ӵ�Bͬʱ��������ÿ��1����λ���ȵ��ٶ��ر�BC���յ�C�˶������˶���ʱ��Ϊt�룬PQ2��y��
����λ���ȵ��ٶ��ر�OA���յ�A�˶�������Q�ӵ�Bͬʱ��������ÿ��1����λ���ȵ��ٶ��ر�BC���յ�C�˶������˶���ʱ��Ϊt�룬PQ2��y��
��1��ֱ��д��y����t�ĺ�������ʽ��t��ȡֵ��Χ���� ����
��2����PQ��![]() ʱ����t��ֵ��
ʱ����t��ֵ��
��3������OB��PQ�ڵ�D����˫����![]() ��k��0��������D����k��ֵ�Ƿ�仯�������仯�������k��ֵ�����仯����˵�����ɣ�
��k��0��������D����k��ֵ�Ƿ�仯�������仯�������k��ֵ�����仯����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
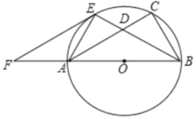
����Ŀ����ͼ����֪��![]() �ı�
�ı�![]() Ϊֱ����
Ϊֱ����![]() �����Բ��
�����Բ��![]() ƽ����
ƽ����![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ���ӳ�����
���ӳ�����![]() ��
��
��1����֤��![]() ��
��![]() ���ߣ�
���ߣ�
��2����![]() ��
��![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
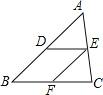
����Ŀ����ͼ������ABC�У�DE��BC��EF��AB�������н�����ȷ���ǣ�������
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABC�У�AB��AC����D��AB��һ�㣬��BDΪֱ���ġ�0��AC�������ڵ�E����BC�ڵ�F��FG��AC�ڵ�G��
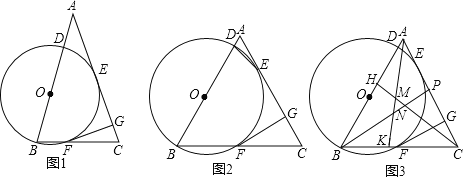
��1����ͼl����֤��GE��GF��
��2����ͼ2������DE����GFC��2��AED����֤����ABCΪ�ȱ������Σ�
��3����ͼ3���ڣ�2���������£���H��K��P�ֱ���AB��BC��AC�ϣ�AK��BP�ֱ�CH�ڵ�M��N��AH��BK����PNC��![]() ��BAK��60����CN��6��CM��4
��BAK��60����CN��6��CM��4![]() ����BC�ij���
����BC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ������
������![]() ��
��![]() ͬʱ�ӵ�
ͬʱ�ӵ�![]() ��������
��������![]() ��
��![]() ���ٶ�������
���ٶ�������![]() �˶�����
�˶�����![]() ����
����![]() ��
��![]() ���ٶ���
���ٶ���![]() �˶�����
�˶�����![]() ����
����![]() ��
��![]() ͬʱ����
ͬʱ����![]() ʱ��
ʱ��![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��
��![]() �ĺ���ͼ�������( )
�ĺ���ͼ�������( )
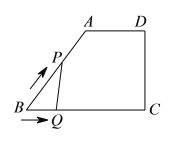
A. 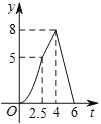 B.
B. 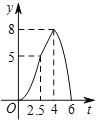
C. 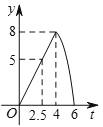 D.
D. 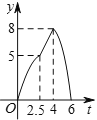
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����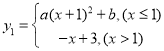 ��
��![]() ������
Ϊ������![]() ������֪��
������֪��![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() ����Ըú�������ͼ���������̽����
����Ըú�������ͼ���������̽����

��1������![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����ͼ������ƽ��ֱ������ϵ�У������ú�����ͼ��
��3�������������ͼ����д���ú�����һ�����ʣ�
��4��������⣺������![]() ��
��![]() ���������������㣬��ֱ��д��
���������������㣬��ֱ��д��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com