
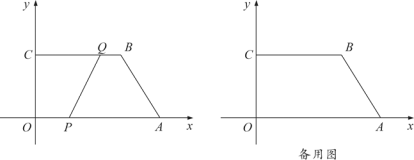
【题目】如图,在平面直角坐标系中,四边形OABC的顶点坐标分别为O(0,0),A(6,0),B(4,3),C(0,3).动点P从点O出发,以每秒![]() 个单位长度的速度沿边OA向终点A运动;动点Q从点B同时出发,以每秒1个单位长度的速度沿边BC向终点C运动.设运动的时间为t秒,PQ2=y.
个单位长度的速度沿边OA向终点A运动;动点Q从点B同时出发,以每秒1个单位长度的速度沿边BC向终点C运动.设运动的时间为t秒,PQ2=y.
(1)直接写出y关于t的函数解析式及t的取值范围: ;
(2)当PQ=![]() 时,求t的值;
时,求t的值;
(3)连接OB交PQ于点D,若双曲线![]() (k≠0)经过点D,问k的值是否变化?若不变化,请求出k的值;若变化,请说明理由.
(k≠0)经过点D,问k的值是否变化?若不变化,请求出k的值;若变化,请说明理由.
【答案】(1)![]() (0≤t≤4);(2)t1=2,t2=
(0≤t≤4);(2)t1=2,t2=![]() ;(3)经过点D的双曲线
;(3)经过点D的双曲线![]() (k≠0)的k值不变,为
(k≠0)的k值不变,为![]() .
.
【解析】
(1)过点P作PE⊥BC于点E,由点P,Q的出发点、速度及方向可找出当运动时间为t秒时点P,Q的坐标,进而可得出PE,EQ的长,再利用勾股定理即可求出y关于t的函数解析式(由时间=路程÷速度可得出t的取值范围);
(2)将PQ=![]() 代入(1)的结论中可得出关于t的一元二次方程,解之即可得出结论;
代入(1)的结论中可得出关于t的一元二次方程,解之即可得出结论;
(3)连接OB,交PQ于点D,过点D作DF⊥OA于点F,求得点D的坐标,再利用反比例函数图象上点的坐标特征即可求出k值,此题得解.
解:(1)过点P作PE⊥BC于点E,如图1所示.
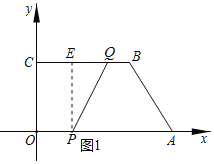
当运动时间为t秒时(0≤t≤4)时,点P的坐标为(![]() t,0),点Q的坐标为(4-t,3),
t,0),点Q的坐标为(4-t,3),
∴PE=3,EQ=|4-t-![]() t|=|4-
t|=|4-![]() t|,
t|,
∴PQ2=PE2+EQ2=32+|4-![]() t|2=
t|2=![]() t2-20t+25,
t2-20t+25,
∴y关于t的函数解析式及t的取值范围:y=![]() t220t+25(0≤t≤4);
t220t+25(0≤t≤4);
故答案为:y=![]() t220t+25(0≤t≤4).
t220t+25(0≤t≤4).
(2)当PQ=![]() 时,
时,![]() t220t+25=(
t220t+25=(![]() )2
)2
整理,得5t2-16t+12=0,
解得:t1=2,t2=![]() .
.
(3)经过点D的双曲线y=![]() (k≠0)的k值不变.
(k≠0)的k值不变.
连接OB,交PQ于点D,过点D作DF⊥OA于点F,如图2所示.
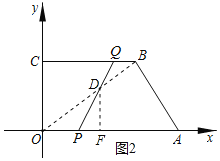
∵OC=3,BC=4,
∴OB=![]() =5.
=5.
∵BQ∥OP,
∴△BDQ∽△ODP,
∴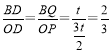 ,
,
∴OD=3.
∵CB∥OA,
∴∠DOF=∠OBC.
在Rt△OBC中,sin∠OBC=![]() ,cos∠OBC=
,cos∠OBC=![]() =
=![]() ,
,
∴OF=ODcos∠OBC=3×![]() =
=![]() ,DF=ODsin∠OBC=3×
,DF=ODsin∠OBC=3×![]() =
=![]() ,
,
∴点D的坐标为(![]() ,
,![]() ),
),
∴经过点D的双曲线y=![]() (k≠0)的k值为
(k≠0)的k值为![]() ×
×![]() =
=![]() ..
..


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
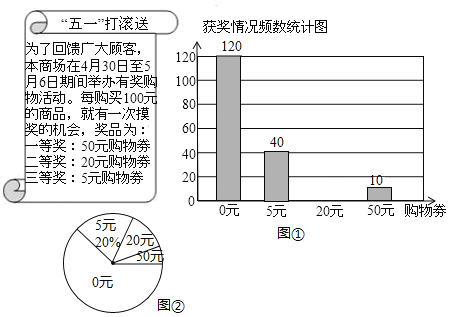
【题目】“五一”期间,新华商场贴出促销海报在商场活动期间,王莉同学随机调查了部分参与活动的顾客,并将调查结果绘制了两幅不完整的统计图请根据图中信息解答下列问题:
(1)王莉同学随机调查的顾客有多少人?
(2)通过计算补全条形统计图;
(3)若商场每天约有2000人次摸奖,请估算商场一天送出的购物券总金额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应上级教委的“海航招飞”号召,某校从九年级应届男生中抽取视力等生理指标合格的部分学生进行了文化课初检,教务处负责同志将测測试结果分为四个等级:甲、乙、丙、丁,然后将相关数据整理为两幅不完整的统计图,请依据相关信息解答下列问题:
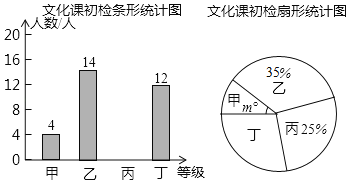
(1)本次参加文化课初检的男生人数为 ;
(2)扇形图中m的数值为 ,把条形统计图补充完整;
(3)据统计,全省生理指标过关的九年级男生有2400名左右,若规定文化课等级为“甲”“乙”的可进行文化课二检,请估计进入二检的男生有 ;
(4)本次抽检进入“甲”等的4名男生中九(1)、九(2)班各占2名,若从“甲”等学生中随机抽取两名男生进行调研,请用树形图表示抽到的两名男生恰为九(1)班的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,BC=12,E为AD中点,F为AB上一点,将△AEF沿EF折叠后,点A恰好落到CF上的点G处,则折痕EF的长是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,□ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:①EO⊥AC;②S△AOD=4S△OCF;③AC:BD=![]() :7;④FB2=OFDF.其中正确的是( )
:7;④FB2=OFDF.其中正确的是( )
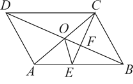
A.①②④B.①③④C.②③④D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
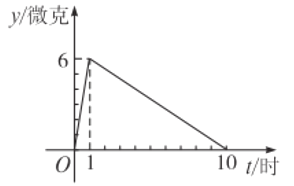
【题目】在抗击新型冠状病毒感染的肺炎疫情过程中,某医药研究所正在试研发一种抑制新型冠状病毒的药物,据临床观察:如果成人按规定的剂量注射这种药物,注射药物后每毫升血液中的含药量![]() (微克)与时间
(微克)与时间![]() (小时)之间的关系近似地满足图中折线.
(小时)之间的关系近似地满足图中折线.
(1)求注射药物后每毫升血液中含药量![]() 与时间
与时间![]() 之间的函数关系式,并写出自变量的取值范围;
之间的函数关系式,并写出自变量的取值范围;
(2)据临床观察:每毫升血液中含药量不少于![]() 微克时,对控制病情是有效的.如果病人按规定的剂量注射 该药物后,求控制病情的有效时间.
微克时,对控制病情是有效的.如果病人按规定的剂量注射 该药物后,求控制病情的有效时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[知识回顾]
七年级学习代数式求值时,遇到这样一类题 “代数式![]() 的值与
的值与![]() 的取值无关,求
的取值无关,求![]() 的值”,通常的解题方法是:把
的值”,通常的解题方法是:把![]() 看作字母,
看作字母,![]() 看作系数合并同类项,因为代数式的值与
看作系数合并同类项,因为代数式的值与![]() 的取值无关,所以含
的取值无关,所以含![]() 项的系数为
项的系数为![]() ,即原式
,即原式![]() ,所以
,所以![]() ,则
,则![]() .
.
[理解应用]
![]() 若关于
若关于![]() 的多项式
的多项式![]() 的值与
的值与![]() 的取值无关,试求
的取值无关,试求![]() 的值:
的值:
![]() 若一次函数
若一次函数![]() 的图像经过某个定点,则该定点坐标为 ;
的图像经过某个定点,则该定点坐标为 ;
[能力提升]
![]() 张如图1的小长方形,长为
张如图1的小长方形,长为![]() ,宽为
,宽为![]() ,按照图2方式不重叠地放在大矩形
,按照图2方式不重叠地放在大矩形![]() 内,大矩形中未被覆盖的两个部分(图中阴影部分) ,设右上角的面积为
内,大矩形中未被覆盖的两个部分(图中阴影部分) ,设右上角的面积为![]() ,左下角的面积为
,左下角的面积为![]() ,当
,当![]() 的长变化时,
的长变化时,![]() 的值始终保持不变,求
的值始终保持不变,求![]() 与
与![]() 的等量关系.
的等量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.

根据以上信息解决下列问题:
(1)![]() ,
,![]() ;
;
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为 ![]() ;
;
(3)从选航模项目的![]() 名学生中随机选取
名学生中随机选取![]() 名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的
名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的![]() 名学生中恰好有
名学生中恰好有![]() 名男生、
名男生、![]() 名女生的概率.
名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一期间,甲、乙两人在附近的景点游玩,甲从![]() 两个景点中任意选择一个游玩,乙从
两个景点中任意选择一个游玩,乙从![]() 三个景点中任意选择一个游玩.
三个景点中任意选择一个游玩.
(1)乙恰好游玩![]() 景点的概率为 .
景点的概率为 .
(2)用列表或画树状图的方法列出甲、乙恰好游玩同一景点的所有等可能的结果.并求甲、乙恰好游玩同一景点的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com