
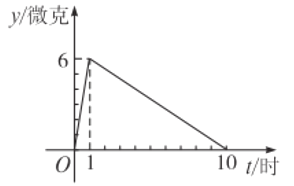
【题目】在抗击新型冠状病毒感染的肺炎疫情过程中,某医药研究所正在试研发一种抑制新型冠状病毒的药物,据临床观察:如果成人按规定的剂量注射这种药物,注射药物后每毫升血液中的含药量![]() (微克)与时间
(微克)与时间![]() (小时)之间的关系近似地满足图中折线.
(小时)之间的关系近似地满足图中折线.
(1)求注射药物后每毫升血液中含药量![]() 与时间
与时间![]() 之间的函数关系式,并写出自变量的取值范围;
之间的函数关系式,并写出自变量的取值范围;
(2)据临床观察:每毫升血液中含药量不少于![]() 微克时,对控制病情是有效的.如果病人按规定的剂量注射 该药物后,求控制病情的有效时间.
微克时,对控制病情是有效的.如果病人按规定的剂量注射 该药物后,求控制病情的有效时间.
【答案】(1)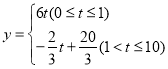 ;(2)
;(2)![]() (小时)
(小时)
【解析】
(1)当0≤t≤1时,是正比例函数,用待定系数法进行求解,即可,当1<t≤10时,是一次函数,用待定系数法求函数的关系式,即可;
(2)当0≤t≤1时,当含药量上升到4微克时,控制病情开始有效,令y=4,代入y=6t,求出对应的t值,同理,当1<t≤10时,求出另一个t值,他们的差就是药的有效时间.
(1)当0≤t≤1时,设y=k1t,则6=k1×1,
∴k1=6,
∴y=6t.
当1<t≤10时,设y=k2t+b,
∴![]() ,解得:
,解得: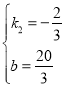 ,
,
∴ y=![]() t+
t+![]() ,
,
综上所述: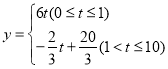 ;
;
(2)当0≤t≤1时,令y=4,即:6t=4,解得:t=![]() ,
,
当0<t≤10时,令y=4,即:![]() t+
t+![]() =4,解得:t=4,
=4,解得:t=4,
∴控制病情的有效时间为:4![]() =
=![]() (小时).
(小时).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于![]() AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )
AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )

A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某建筑物的顶部有一块标识牌 CD,小明在斜坡上 B 处测得标识牌顶部C 的仰角为 45°, 沿斜坡走下来在地面 A 处测得标识牌底部 D 的仰角为 60°,已知斜坡 AB 的坡角为 30°,AB=AE=10 米.则标识牌 CD 的高度是( )米.
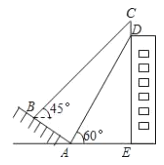
A.15-5![]() B.20-10
B.20-10![]() C.10-5
C.10-5![]() D.5
D.5![]() -5
-5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC和△CDE都是等腰三角形,∠BAC=∠EDC=120°.
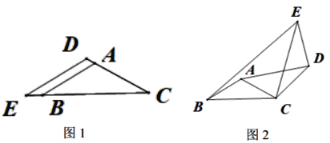
(1)如图1,A、D、C在同一直线上时,![]() =_______,
=_______,![]() =_______;
=_______;
(2)在图1的基础上,固定△ABC,将△CDE绕C旋转一定的角度α(0°<α<360°),如图2,连接AD、BE.
① ![]() 的值有没有改变?请说明理由.
的值有没有改变?请说明理由.
②拓展研究:若AB=1,DE=![]() ,当 B、D、E在同一直线上时,请计算线段AD的长;
,当 B、D、E在同一直线上时,请计算线段AD的长;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OABC的顶点坐标分别为O(0,0),A(6,0),B(4,3),C(0,3).动点P从点O出发,以每秒![]() 个单位长度的速度沿边OA向终点A运动;动点Q从点B同时出发,以每秒1个单位长度的速度沿边BC向终点C运动.设运动的时间为t秒,PQ2=y.
个单位长度的速度沿边OA向终点A运动;动点Q从点B同时出发,以每秒1个单位长度的速度沿边BC向终点C运动.设运动的时间为t秒,PQ2=y.
(1)直接写出y关于t的函数解析式及t的取值范围: ;
(2)当PQ=![]() 时,求t的值;
时,求t的值;
(3)连接OB交PQ于点D,若双曲线![]() (k≠0)经过点D,问k的值是否变化?若不变化,请求出k的值;若变化,请说明理由.
(k≠0)经过点D,问k的值是否变化?若不变化,请求出k的值;若变化,请说明理由.
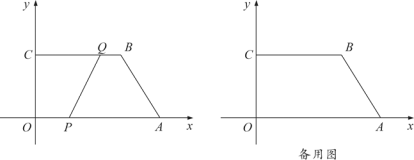
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线的顶点坐标为(0,1)且经过点A(1,2),直线y=3x﹣4![]() 经过点B(
经过点B(![]() ,n),与y轴交点为C.
,n),与y轴交点为C.
(1)求抛物线的解析式及n的值;
(2)将直线BC绕原点O逆时针旋转45°,求旋转后的直线的解析式;
(3)如图2将抛物线绕原点O顺时针旋转45°得到新曲线,新曲线与直线BC交于点M、N,点M在点N的上方,求点N的坐标.
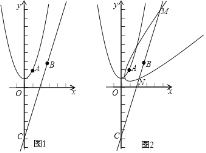
查看答案和解析>>
科目:初中数学 来源: 题型:
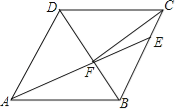
【题目】如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,CE=2,连接CF,以下结论:①△ABF≌△CBF;②点E到AB的距离是2![]() ;③tan∠DCF=
;③tan∠DCF=![]() ;④△ABF的面积为
;④△ABF的面积为![]() .其中一定成立的是 (把所有正确结论的序号都填在横线上).
.其中一定成立的是 (把所有正确结论的序号都填在横线上).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com