
【题目】如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,CE=2,连接CF,以下结论:①△ABF≌△CBF;②点E到AB的距离是2![]() ;③tan∠DCF=
;③tan∠DCF=![]() ;④△ABF的面积为
;④△ABF的面积为![]() .其中一定成立的是 (把所有正确结论的序号都填在横线上).
.其中一定成立的是 (把所有正确结论的序号都填在横线上).
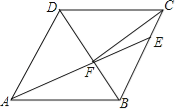
【答案】①②③
【解析】
试题∵ 四边形ABCD是菱形,∴AB=BC=6,
∵∠DAB=60°,∴AB=AD=DB,∠ABD=∠DBC=60°,
在△ABF与△CBF中,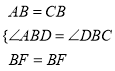 ,
,
∴△ABF≌△CBF(SAS),
∴①正确;
过点E作EG⊥AB,过点F作MH⊥CD,MH⊥AB,如图:
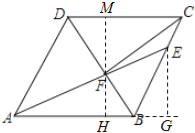
∵CE=2,BC=6,∠ABC=120°,
∴BE=6﹣2=4,
∵EG⊥AB,
∴EG=![]() ,
,
∴点E到AB的距离是![]() ,
,
故②正确;
∵BE=4,EC=2,
∴S△BFE:S△FEC=4:2=2:1,
∴S△ABF:S△FBE=3:2,
∴△ABF的面积为=![]() ,
,
故④错误;
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴FM=![]() ,
,
∴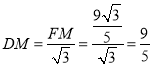 ,
,
∴CM=DC﹣DM=6﹣![]() =
=![]() ,
,
∴tan∠DCF=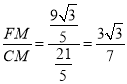 ,
,
故③正确;
故答案为①②③


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:初中数学 来源: 题型:
【题目】为了了解学生对“预防新型冠状病毒”知识的掌握情况,学校组织了一次线上知识培训,培训结束后进行测试,在全校2000名学生中,分别抽取了男生,女生各15份成绩,整理分析过程如下,请补充完整.
(收集数据)
15名男生测试成绩统计如下:(满分100分)78,90,99,93,92,95,94,100,90,85,86,95,75,88,90
15名女生测试成绩统计如下:(满分100分)77,82,83,86,90,90,92,91,93,92,92,92,92,98,100
(整理、描述数据)
70.5~75.5 | 75.5~80.5 | 80.5~85.5 | 85.5~90.5 | 90.5~95.5 | 95.5~100.5 | |
男生 | 1 | 1 | 1 | 5 | 5 | 2 |
女生 | 0 | 1 | 2 | 3 | 7 | 2 |
(分析数据)
(1)两组样本数据的平均数、众数、中位数、方差如下表所示:
性别 | 平均数 | 众数 | 中位数 | 方差 |
男生 | 90 | 90 | 90 | 44.9 |
女生 | 90 |
|
| 32.8 |
在表中:![]() ________.
________.![]() ________;
________;
(2)若规定得分在80分以上(不含80分)为合格,请估计全校学生中“预防新型冠状病毒”知识测试合格的学生有多少人?
(3)通过数据分析得到的结论,你认为男生和女生中谁的成绩比较好?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
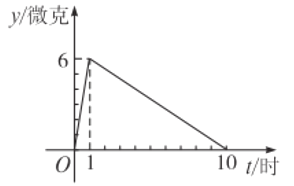
【题目】在抗击新型冠状病毒感染的肺炎疫情过程中,某医药研究所正在试研发一种抑制新型冠状病毒的药物,据临床观察:如果成人按规定的剂量注射这种药物,注射药物后每毫升血液中的含药量![]() (微克)与时间
(微克)与时间![]() (小时)之间的关系近似地满足图中折线.
(小时)之间的关系近似地满足图中折线.
(1)求注射药物后每毫升血液中含药量![]() 与时间
与时间![]() 之间的函数关系式,并写出自变量的取值范围;
之间的函数关系式,并写出自变量的取值范围;
(2)据临床观察:每毫升血液中含药量不少于![]() 微克时,对控制病情是有效的.如果病人按规定的剂量注射 该药物后,求控制病情的有效时间.
微克时,对控制病情是有效的.如果病人按规定的剂量注射 该药物后,求控制病情的有效时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AD∥BC,AD=2BC,点E为AD的中点,连接BE、BD,∠ABD=90°.

(1)如图l,求证:四边形BCDE为菱形;
(2)如图2,连接AC交BD于点F,连接EF,若AC平分∠BAD,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于△ABC面积的![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.

根据以上信息解决下列问题:
(1)![]() ,
,![]() ;
;
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为 ![]() ;
;
(3)从选航模项目的![]() 名学生中随机选取
名学生中随机选取![]() 名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的
名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的![]() 名学生中恰好有
名学生中恰好有![]() 名男生、
名男生、![]() 名女生的概率.
名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司开发处一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为10元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘制成图象,图中的折线ABC表示日销售量y(件)与销售时间x(天)之间的函数关系.

(1)求y与x之间的函数表达式,并写出x的取值范围;
(2)若该节能产品的日销售利润为W(元),求W与x之间的函数表达式,并求出日销售利润不超过1040元的天数共有多少天?
(3)若5≤x≤17,直接写出第几天的日销售利润最大,最大日销售利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校数学兴趣小组的同学测量一架无人飞机P的高度,如图,A,B两个观测点相距![]() ,在A处测得P在北偏东71°方向上,同时在B处测得P在北偏东35°方向上.求无人飞机P离地面的高度.(结果精确到1米,参考数据:
,在A处测得P在北偏东71°方向上,同时在B处测得P在北偏东35°方向上.求无人飞机P离地面的高度.(结果精确到1米,参考数据:![]() ,
,![]() ,sin71°≈0.95,tan71°≈2.90)
,sin71°≈0.95,tan71°≈2.90)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(3,m),B(﹣2,﹣3)是直线AB和某反比例函数的图象的两个交点.
(1)求直线AB和反比例函数的解析式;
(2)观察图象,直接写出当x满足什么范围时,直线AB在双曲线的下方;
(3)反比例函数的图象上是否存在点C,使得△OBC的面积等于△OAB的面积?如果不存在,说明理由;如果存在,求出满足条件的所有点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个圆形转盘,分黑色、白色两个区域.
(1)某人转动转盘,对指针落在黑色区域或白色区域进行了大量试验,得到数据如下表:
实验次数 | 10 | 100 | 2000 | 5000 | 10000 | 50000 | 100000 |
白色区域次数 | 3 | 34 | 680 | 1600 | 3405 | 16500 | 33000 |
落在白色区域频率 | 0.3 | 0.34 | 0.34 | 0.32 | 0.34 | 0.33 | 0.33 |
请你利用上述实验,估计转动该转盘指针落在白色区域的概率为___________.(精确到0.01);
(2)若该圆形转盘白色扇形的圆心角为120度,黑色扇形的圆心角为![]() ,转动转盘两次,求指针一次落在白色区域,另一次落在黑色区域的概率.
,转动转盘两次,求指针一次落在白色区域,另一次落在黑色区域的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com