
ЁОЬтФПЁПЁїABCКЭЁїCDEЖМЪЧЕШбќШ§НЧаЮЃЌЁЯBACЃНЁЯEDCЃН120ЁуЃЎ
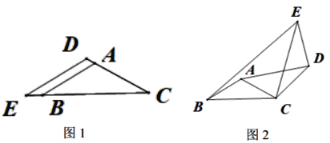
ЃЈ1ЃЉШчЭМ1ЃЌAЁЂDЁЂCдкЭЌвЛжБЯпЩЯЪБЃЌ![]() ЃН_______ЃЌ
ЃН_______ЃЌ![]() ЃН_______ЃЛ
ЃН_______ЃЛ
ЃЈ2ЃЉдкЭМ1ЕФЛљДЁЩЯЃЌЙЬЖЈЁїABCЃЌНЋЁїCDEШЦCа§зЊвЛЖЈЕФНЧЖШІС(0ЁуЃМІСЃМ360Ёу)ЃЌШчЭМ2ЃЌСЌНгADЁЂBEЃЎ
Ђй ![]() ЕФжЕгаУЛгаИФБфЃПЧыЫЕУїРэгЩЃЎ
ЕФжЕгаУЛгаИФБфЃПЧыЫЕУїРэгЩЃЎ
ЂкЭиеЙбаОПЃКШєABЃН1ЃЌDEЃН![]() ЃЌЕБ BЁЂDЁЂEдкЭЌвЛжБЯпЩЯЪБЃЌЧыМЦЫуЯпЖЮADЕФГЄЃЛ
ЃЌЕБ BЁЂDЁЂEдкЭЌвЛжБЯпЩЯЪБЃЌЧыМЦЫуЯпЖЮADЕФГЄЃЛ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЌ
ЃЌ![]() ЃЛЃЈ2ЃЉЂйУЛгаИФБфЃЌРэгЩМћНтЮіЃЛЂкЯпЖЮADЕФГЄЮЊ
ЃЛЃЈ2ЃЉЂйУЛгаИФБфЃЌРэгЩМћНтЮіЃЛЂкЯпЖЮADЕФГЄЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЕШбќШ§НЧаЮЕФаджЪКЭжБНЧШ§НЧаЮЕФаджЪПЩЕУACЃН2AHЃЌCHЃН![]() AHЃЌгЩЦНааЯпЗжЯпЖЮГЩБШР§ПЩЕУ
AHЃЌгЩЦНааЯпЗжЯпЖЮГЩБШР§ПЩЕУ![]() ЃЌМДПЩЧѓНтЃЛ
ЃЌМДПЩЧѓНтЃЛ
ЃЈ2ЃЉЂйЭЈЙ§жЄУїЁїACDЁзЁїBCEЃЌПЩЕУ![]() ЃЛЂкЗжСНжжЧщПіНјааЬжТлЃЌЃЈiЃЉШчЭМЃЌЕБBЁЂDЁЂEдкЭЌвЛжБЯпЩЯЃЌЧвЕуDдкBEжаМфЪБЃЌЙ§ЕуCзїCNЁЭBEгкNЃЌРћгУжБНЧШ§НЧаЮЕФаджЪКЭЙДЙЩЖЈРэЧѓГіBEЃН
ЃЛЂкЗжСНжжЧщПіНјааЬжТлЃЌЃЈiЃЉШчЭМЃЌЕБBЁЂDЁЂEдкЭЌвЛжБЯпЩЯЃЌЧвЕуDдкBEжаМфЪБЃЌЙ§ЕуCзїCNЁЭBEгкNЃЌРћгУжБНЧШ§НЧаЮЕФаджЪКЭЙДЙЩЖЈРэЧѓГіBEЃН![]() ЃЌгЩЂйЕФНсТлПЩЧѓНтЃЛЃЈiiЃЉШчЭМЃЌЕБ BЁЂDЁЂEдкЭЌвЛжБЯпЩЯЃЌЧвЕуBдкEDжаМфЪБЃЌЙ§ЕуBзїBHЁЭECгкHЃЌРћгУЙДЙЩЖЈРэЧѓГіBHЃН
ЃЌгЩЂйЕФНсТлПЩЧѓНтЃЛЃЈiiЃЉШчЭМЃЌЕБ BЁЂDЁЂEдкЭЌвЛжБЯпЩЯЃЌЧвЕуBдкEDжаМфЪБЃЌЙ§ЕуBзїBHЁЭECгкHЃЌРћгУЙДЙЩЖЈРэЧѓГіBHЃН![]() ЃЌдйгЩЂйЕФНсТлПЩЧѓНтЃЎ
ЃЌдйгЩЂйЕФНсТлПЩЧѓНтЃЎ
НтЃКЃЈ1ЃЉШчЭМ1ЃЌЙ§ЕуAзїAHЁЭBCгкHЃЌ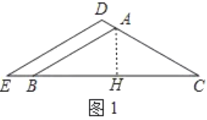
ЁпЁЯBACЃН120ЁуЃЌABЃНACЃЌAHЁЭBCЃЌ
ЁрЁЯABCЃНЁЯACBЃН30ЁуЃЌBHЃНCHЃЌ
ЁрACЃН2AHЃЌCHЃН![]() ЃЌ
ЃЌ
ЁрBCЃН2![]() AHЃЌ
AHЃЌ
ЁпЁЯBACЃНЁЯEDCЃН120ЁуЃЌ
ЁрABЁЮDEЃЌ
Ёр![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊЃК![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЂйУЛгаИФБфЃЌ
РэгЩШчЯТЃКЁпНЋЁїCDEШЦCа§зЊвЛЖЈЕФНЧЖШІСЃЈ0ЁуЃМІСЃМ360ЁуЃЉЃЌ
ЁрЁЯACDЃНЁЯBCEЃЌ
ЁпABЃНACЃЌDEЃНCDЃЌ
Ёр![]() ЃЌЧвЁЯBACЃНЁЯEDCЃН120ЁуЃЌ
ЃЌЧвЁЯBACЃНЁЯEDCЃН120ЁуЃЌ
ЁрЁїABCЁзЁїDECЃЌ
Ёр![]() ЃЌЧвЁЯACDЃНЁЯBCEЃЌ
ЃЌЧвЁЯACDЃНЁЯBCEЃЌ
ЁрЁїACDЁзЁїBCEЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЕФжЕгаУЛгаИФБф
ЕФжЕгаУЛгаИФБф
ЂкЃЈiЃЉШчЭМЃЌЕБBЁЂDЁЂEдкЭЌвЛжБЯпЩЯЃЌЧвЕуDдкBEжаМфЪБЃЌЙ§ЕуCзїCNЁЭBEгкNЃЌ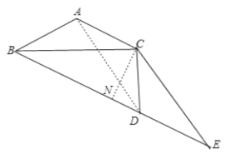
ЁпACЃНABЃН1ЃЌ
ЁргЩЃЈ1ЃЉПЩжЊЃЌBCЃН![]() ЃЌ
ЃЌ
ЁпЁЯCDEЃН120ЁуЃЌ
ЁрЁЯBDCЃН60ЁуЃЌЧвCDЃНDEЃН![]() ЃЌCNЁЭBEЃЌ
ЃЌCNЁЭBEЃЌ
ЁрDNЃН![]() CDЃН
CDЃН![]() ЃЌCNЃН
ЃЌCNЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрEC=2CN=![]() ЃЌ
ЃЌ
ЁпBNЃН![]() ЃЌ
ЃЌ
ЁрBEЃН![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
ЁрADЃН![]() ЃЌ
ЃЌ
ЃЈiiЃЉШчЭМЃЌЕБ BЁЂDЁЂEдкЭЌвЛжБЯпЩЯЃЌЧвЕуBдкEDжаМфЪБЃЌЙ§ЕуBзїBHЁЭECгкHЃЌ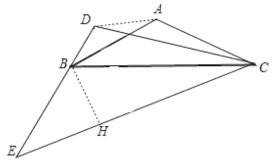
ЁпЁЯBECЃН30ЁуЃЌBHЁЭECЃЌ
ЁрBE=2BHЃЌEHЃН![]() ЃЌ
ЃЌ
ЁпBC2ЃНBH2ЃЋHC2ЃЌ
Ёр3ЃНBH2ЃЋ![]() ЃЌ
ЃЌ
ЁрBHЃН![]() ЃЌ
ЃЌ
ЁрBEЃН![]()
Ёп![]()
ЁрADЃН![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃЌЯпЖЮADЕФГЄЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЋЫОМЦЛЎЙКТђ![]() ЁЂ
ЁЂ![]() СНжжаЭКХЕФЛњЦїШЫАсдЫВФСЯЃЌвбжЊ
СНжжаЭКХЕФЛњЦїШЫАсдЫВФСЯЃЌвбжЊ![]() аЭЛњЦїШЫБШ
аЭЛњЦїШЫБШ![]() аЭЛњЦїШЫУПаЁЪБЖрАсдЫ
аЭЛњЦїШЫУПаЁЪБЖрАсдЫ![]() ВФСЯЃЌЧв
ВФСЯЃЌЧв![]() аЭЛњЦїШЫАсдЫ
аЭЛњЦїШЫАсдЫ![]() ЕФВФСЯЫљгУЕФЪБМфгы
ЕФВФСЯЫљгУЕФЪБМфгы![]() аЭЛњЦїШЫАсдЫ
аЭЛњЦїШЫАсдЫ![]() ВФСЯЫљгУЕФЪБМфЯрЭЌЃЎ
ВФСЯЫљгУЕФЪБМфЯрЭЌЃЎ
ЃЈ1ЃЉЧѓ![]() ЁЂ
ЁЂ![]() СНжжаЭКХЕФЛњЦїШЫУПаЁЪБЗжБ№АсдЫЖрЩйВФСЯЃП
СНжжаЭКХЕФЛњЦїШЫУПаЁЪБЗжБ№АсдЫЖрЩйВФСЯЃП
ЃЈ2ЃЉИУЙЋЫОМЦЛЎВЩЙК![]() ЁЂ
ЁЂ![]() СНжжаЭКХЕФЛњЦїШЫЙВ
СНжжаЭКХЕФЛњЦїШЫЙВ![]() ЬЈЃЌвЊЧѓУПаЁЪБАсдЫЕФВФСЯВЛЕУЩйгк
ЬЈЃЌвЊЧѓУПаЁЪБАсдЫЕФВФСЯВЛЕУЩйгк![]() ЃЌдђжСЩйЙКНј
ЃЌдђжСЩйЙКНј![]() аЭЛњЦїШЫЖрЩйЬЈЃП
аЭЛњЦїШЫЖрЩйЬЈЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫСЫНтбЇЩњЖдЁАдЄЗРаТаЭЙкзДВЁЖОЁБжЊЪЖЕФеЦЮеЧщПіЃЌбЇаЃзщжЏСЫвЛДЮЯпЩЯжЊЪЖХрбЕЃЌХрбЕНсЪјКѓНјааВтЪдЃЌдкШЋаЃ2000УћбЇЩњжаЃЌЗжБ№ГщШЁСЫФаЩњЃЌХЎЩњИї15ЗнГЩМЈЃЌећРэЗжЮіЙ§ГЬШчЯТЃЌЧыВЙГфЭъећЃЎ
ЃЈЪеМЏЪ§ОнЃЉ
15УћФаЩњВтЪдГЩМЈЭГМЦШчЯТЃКЃЈТњЗж100ЗжЃЉ78ЃЌ90ЃЌ99ЃЌ93ЃЌ92ЃЌ95ЃЌ94ЃЌ100ЃЌ90ЃЌ85ЃЌ86ЃЌ95ЃЌ75ЃЌ88ЃЌ90
15УћХЎЩњВтЪдГЩМЈЭГМЦШчЯТЃКЃЈТњЗж100ЗжЃЉ77ЃЌ82ЃЌ83ЃЌ86ЃЌ90ЃЌ90ЃЌ92ЃЌ91ЃЌ93ЃЌ92ЃЌ92ЃЌ92ЃЌ92ЃЌ98ЃЌ100
ЃЈећРэЁЂУшЪіЪ§ОнЃЉ
70.5ЁЋ75.5 | 75.5ЁЋ80.5 | 80.5ЁЋ85.5 | 85.5ЁЋ90.5 | 90.5ЁЋ95.5 | 95.5ЁЋ100.5 | |
ФаЩњ | 1 | 1 | 1 | 5 | 5 | 2 |
ХЎЩњ | 0 | 1 | 2 | 3 | 7 | 2 |
ЃЈЗжЮіЪ§ОнЃЉ
ЃЈ1ЃЉСНзщбљБОЪ§ОнЕФЦНОљЪ§ЁЂжкЪ§ЁЂжаЮЛЪ§ЁЂЗНВюШчЯТБэЫљЪОЃК
адБ№ | ЦНОљЪ§ | жкЪ§ | жаЮЛЪ§ | ЗНВю |
ФаЩњ | 90 | 90 | 90 | 44.9 |
ХЎЩњ | 90 |
|
| 32.8 |
дкБэжаЃК![]() ________ЃЎ
________ЃЎ![]() ________ЃЛ
________ЃЛ
ЃЈ2ЃЉШєЙцЖЈЕУЗждк80ЗжвдЩЯЃЈВЛКЌ80ЗжЃЉЮЊКЯИёЃЌЧыЙРМЦШЋаЃбЇЩњжаЁАдЄЗРаТаЭЙкзДВЁЖОЁБжЊЪЖВтЪдКЯИёЕФбЇЩњгаЖрЩйШЫЃП
ЃЈ3ЃЉЭЈЙ§Ъ§ОнЗжЮіЕУЕНЕФНсТлЃЌФуШЯЮЊФаЩњКЭХЎЩњжаЫЕФГЩМЈБШНЯКУЃПЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃМЦЛЎзщжЏбЇЩњВЮМгЁАЪщЗЈЁБЁЂЁАЩугАЁБЁЂЁАКНФЃЁБЁЂЁАЮЇЦхЁБЫФИіПЮЭтаЫШЄаЁзщЃЌвЊЧѓУПШЫБиаыВЮМгЃЌВЂЧвжЛФмбЁдёЦфжавЛИіаЁзщЃЌЮЊСЫНтбЇЩњЖдЫФИіПЮЭтаЫШЄаЁзщЕФбЁдёЧщПіЃЌбЇаЃДгШЋЬхбЇЩњжаЫцЛњГщШЁВПЗжбЇЩњНјааЮЪОэЕїВщЃЌВЂАбЕїВщНсЙћжЦГЩШчЭМЫљЪОЕФЩШаЮЭГМЦЭМКЭЬѕаЮЭГМЦЭМ(ВПЗжаХЯЂЮДИјГі)ЃЌЧыФуИљОнИјГіЕФаХЯЂНтД№ЯТСаЮЪЬтЃК

ЃЈ1ЃЉЧѓВЮМгетДЮЮЪОэЕїВщЕФбЇЩњШЫЪ§ЃЌВЂВЙШЋЬѕаЮЭГМЦЭМ(ЛЭМКѓЧыБъзЂЯргІЕФЪ§Он)ЃЛ
ЃЈ2ЃЉmЃН_______ЃЌnЃН_______ЃЛ
ЃЈ3ЃЉШєИУаЃЙВга1200УћбЇЩњЃЌЪдЙРМЦИУаЃбЁдёЁАЮЇЦхЁБПЮЭтаЫШЄаЁзщЕФбЇЩњгаЖрЩйШЫЃП
ЃЈ4ЃЉЗжБ№гУAЁЂBЁЂCЁЂDБэЪОЁАЪщЗЈЁБЁЂЁАЩугАЁБЁЂЁАКНФЃЁБЁЂЁАЮЇЦхЁБЃЌаЁУїКЭаЁКьДгжаИїбЁШЁвЛИіаЁзщЃЌЧыгУЪїзДЭМЗЈЛђСаБэЗЈЧѓГіЁАСНШЫбЁдёаЁзщВЛЭЌЁБЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDжаЃЌABЃН8ЃЌBCЃН12ЃЌEЮЊADжаЕуЃЌFЮЊABЩЯвЛЕуЃЌНЋЁїAEFбиEFелЕўКѓЃЌЕуAЧЁКУТфЕНCFЩЯЕФЕуGДІЃЌдђелКлEFЕФГЄЪЧ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙњМвМЦЛЎ2035ФъЧАЪЕЪЉаТФмдДЦћГЕЃЌФГЙЋЫОЮЊМгПьаТОЩЖЏФмзЊЛЛЃЌЬсИпЙЋЫООМУаЇвцЃЌОіЖЈЖдНќЦкбаЗЂГіЕФвЛжжаТаЭФмдДВњЦЗНјааНЕМлДйЯњ.ИљОнЪаГЁЕїВщЃКетжжаТаЭФмдДВњЦЗЯњЪлЕЅМлЖЈЮЊ200дЊЪБЃЌУПЬьПЩЪлГі300ИіЃЛШєЯњЪлЕЅМлУПНЕЕЭ1дЊЃЌУПЬьПЩЖрЪлГі5Иі.вбжЊУПИіаТаЭФмдДВњЦЗЕФГЩБОЮЊ100дЊ.
ЮЪЃКЃЈ1ЃЉЩшИУВњЦЗЕФЯњЪлЕЅМлЮЊ![]() дЊЃЌУПЬьЕФРћШѓЮЊ
дЊЃЌУПЬьЕФРћШѓЮЊ![]() дЊ.дђ
дЊ.дђ![]() _________ЃЈгУКЌ
_________ЃЈгУКЌ![]() ЕФДњЪ§ЪНБэЪОЃЉ
ЕФДњЪ§ЪНБэЪОЃЉ
ЃЈ2ЃЉетжжаТаЭФмдДВњЦЗНЕМлКѓЕФЯњЪлЕЅМлЮЊЖрЩйдЊЪБЃЌЙЋЫОУПЬьПЩЛёРћ32000дЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
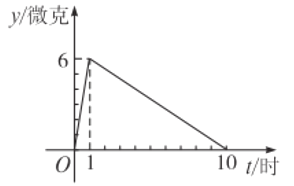
ЁОЬтФПЁПдкПЙЛїаТаЭЙкзДВЁЖОИаШОЕФЗЮбзвпЧщЙ§ГЬжаЃЌФГвНвЉбаОПЫље§дкЪдбаЗЂвЛжжвжжЦаТаЭЙкзДВЁЖОЕФвЉЮяЃЌОнСйДВЙлВьЃКШчЙћГЩШЫАДЙцЖЈЕФМССПзЂЩфетжжвЉЮяЃЌзЂЩфвЉЮяКѓУПКСЩ§бЊвКжаЕФКЌвЉСП![]() ЃЈЮЂПЫ)гыЪБМф
ЃЈЮЂПЫ)гыЪБМф![]() (аЁЪБ)жЎМфЕФЙиЯЕНќЫЦЕиТњзуЭМжаелЯпЃЎ
(аЁЪБ)жЎМфЕФЙиЯЕНќЫЦЕиТњзуЭМжаелЯпЃЎ
ЃЈ1ЃЉЧѓзЂЩфвЉЮяКѓУПКСЩ§бЊвКжаКЌвЉСП![]() гыЪБМф
гыЪБМф![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСПЕФШЁжЕЗЖЮЇЃЛ
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСПЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉОнСйДВЙлВьЃКУПКСЩ§бЊвКжаКЌвЉСПВЛЩйгк![]() ЮЂПЫЪБЃЌЖдПижЦВЁЧщЪЧгааЇЕФЃЎШчЙћВЁШЫАДЙцЖЈЕФМССПзЂЩф ИУвЉЮяКѓЃЌЧѓПижЦВЁЧщЕФгааЇЪБМфЃЎ
ЮЂПЫЪБЃЌЖдПижЦВЁЧщЪЧгааЇЕФЃЎШчЙћВЁШЫАДЙцЖЈЕФМССПзЂЩф ИУвЉЮяКѓЃЌЧѓПижЦВЁЧщЕФгааЇЪБМфЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЫФБпаЮABCDжаЃЌADЁЮBCЃЌADЃН2BCЃЌЕуEЮЊADЕФжаЕуЃЌСЌНгBEЁЂBDЃЌЁЯABDЃН90ЁуЃЎ

ЃЈ1ЃЉШчЭМlЃЌЧѓжЄЃКЫФБпаЮBCDEЮЊСтаЮЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌСЌНгACНЛBDгкЕуFЃЌСЌНгEFЃЌШєACЦНЗжЁЯBADЃЌдкВЛЬэМгШЮКЮИЈжњЯпЕФЧщПіЯТЃЌЧыжБНгаДГіЭМ2жаЫФИіШ§НЧаЮЃЌЪЙаДГіЕФУПИіШ§НЧаЮЕФУцЛ§ЖМЕШгкЁїABCУцЛ§ЕФ![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊAЃЈ3ЃЌmЃЉЃЌBЃЈЉ2ЃЌЉ3ЃЉЪЧжБЯпABКЭФГЗДБШР§КЏЪ§ЕФЭМЯѓЕФСНИіНЛЕуЃЎ
ЃЈ1ЃЉЧѓжБЯпABКЭЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЙлВьЭМЯѓЃЌжБНгаДГіЕБxТњзуЪВУДЗЖЮЇЪБЃЌжБЯпABдкЫЋЧњЯпЕФЯТЗНЃЛ
ЃЈ3ЃЉЗДБШР§КЏЪ§ЕФЭМЯѓЩЯЪЧЗёДцдкЕуCЃЌЪЙЕУЁїOBCЕФУцЛ§ЕШгкЁїOABЕФУцЛ§ЃПШчЙћВЛДцдкЃЌЫЕУїРэгЩЃЛШчЙћДцдкЃЌЧѓГіТњзуЬѕМўЕФЫљгаЕуCЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com