
ЁОЬтФПЁПФГаЃМЦЛЎзщжЏбЇЩњВЮМгЁАЪщЗЈЁБЁЂЁАЩугАЁБЁЂЁАКНФЃЁБЁЂЁАЮЇЦхЁБЫФИіПЮЭтаЫШЄаЁзщЃЌвЊЧѓУПШЫБиаыВЮМгЃЌВЂЧвжЛФмбЁдёЦфжавЛИіаЁзщЃЌЮЊСЫНтбЇЩњЖдЫФИіПЮЭтаЫШЄаЁзщЕФбЁдёЧщПіЃЌбЇаЃДгШЋЬхбЇЩњжаЫцЛњГщШЁВПЗжбЇЩњНјааЮЪОэЕїВщЃЌВЂАбЕїВщНсЙћжЦГЩШчЭМЫљЪОЕФЩШаЮЭГМЦЭМКЭЬѕаЮЭГМЦЭМ(ВПЗжаХЯЂЮДИјГі)ЃЌЧыФуИљОнИјГіЕФаХЯЂНтД№ЯТСаЮЪЬтЃК

ЃЈ1ЃЉЧѓВЮМгетДЮЮЪОэЕїВщЕФбЇЩњШЫЪ§ЃЌВЂВЙШЋЬѕаЮЭГМЦЭМ(ЛЭМКѓЧыБъзЂЯргІЕФЪ§Он)ЃЛ
ЃЈ2ЃЉmЃН_______ЃЌnЃН_______ЃЛ
ЃЈ3ЃЉШєИУаЃЙВга1200УћбЇЩњЃЌЪдЙРМЦИУаЃбЁдёЁАЮЇЦхЁБПЮЭтаЫШЄаЁзщЕФбЇЩњгаЖрЩйШЫЃП
ЃЈ4ЃЉЗжБ№гУAЁЂBЁЂCЁЂDБэЪОЁАЪщЗЈЁБЁЂЁАЩугАЁБЁЂЁАКНФЃЁБЁЂЁАЮЇЦхЁБЃЌаЁУїКЭаЁКьДгжаИїбЁШЁвЛИіаЁзщЃЌЧыгУЪїзДЭМЗЈЛђСаБэЗЈЧѓГіЁАСНШЫбЁдёаЁзщВЛЭЌЁБЕФИХТЪЃЎ
ЁОД№АИЁПЃЈ1ЃЉВЮМгетДЮЮЪОэЕїВщЕФбЇЩњШЫЪ§150ШЫЃЌЭМаЮМћНтЮіЃЛЃЈ2ЃЉ36ЁЂ16ЃЛЃЈ3ЃЉИУаЃбЁдёЁАЮЇЦхЁБПЮЭтаЫШЄаЁзщЕФбЇЩњга192ШЫЃЛЃЈ4ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЪщЗЈаЁзщШЫЪ§МАЦфЖдгІАйЗжБШПЩЕУзмШЫЪ§ЃЌдйИљОнИїаЁзщШЫЪ§жЎКЭЕШгкзмШЫЪ§ЧѓЕУКНФЃШЫЪ§ЃЌДгЖјВЙШЋЭМаЮЃЛ
ЃЈ2ЃЉИљОнАйЗжБШЕФИХФюПЩЕУmЁЂnЕФжЕЃЛ
ЃЈ3ЃЉзмШЫЪ§ГЫвдбљБОжаЮЇЦхЕФШЫЪ§ЫљеМАйЗжБШЃЛ
ЃЈ4ЃЉИљОнЬтвтЛГіЪїзДЭМЕУГіЫљгаЕШЧщПіЪ§КЭЁАСНШЫбЁдёаЁзщВЛЭЌЁБЕФЧщПіЪ§ЃЌдйИљОнИХТЪЙЋЪНМДПЩЕУГіД№АИЃЎ
НтЃКЃЈ1ЃЉВЮМгетДЮЮЪОэЕїВщЕФбЇЩњШЫЪ§ЮЊЃК30ЁТ20%ЃН150ЃЈШЫЃЉЃЌ
КНФЃЕФШЫЪ§ЮЊ150ЃЈ30ЃЋ54ЃЋ24ЃЉЃН42ЃЈШЫЃЉЃЌ
ВЙШЋЭМаЮШчЯТЃК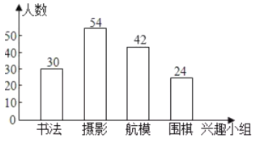
ЃЈ2ЃЉm%ЃН![]() ЃЌn%ЃН
ЃЌn%ЃН![]() ЃЌ
ЃЌ
МДmЃН36ЃЌnЃН16ЃЌ
ЙЪД№АИЮЊЃК36ЁЂ16ЃЛ
ЃЈ3ЃЉИУаЃбЁдёЁАЮЇЦхЁБПЮЭтаЫШЄаЁзщЕФбЇЩњга1200ЁС16%ЃН192ЃЈШЫЃЉЃЛ
ЃЈ4ЃЉИљОнЬтвтЛЭМШчЯТЃК
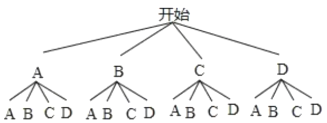
ЙВга16жжЕШЧщПіЪ§ЃЌЦфжаЁАСНШЫбЁдёаЁзщВЛЭЌЁБЕФга12жжЃЌ
дђЁАСНШЫбЁдёаЁзщВЛЭЌЁБЕФИХТЪЪЧ![]() ЃЎ
ЃЎ


 аТБраЁбЇЕЅдЊздВтЬтЯЕСаД№АИ
аТБраЁбЇЕЅдЊздВтЬтЯЕСаД№АИ зжДЪОфЖЮЦЊЯЕСаД№АИ
зжДЪОфЖЮЦЊЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§yЃНax2ЃЋbxЃЋcЕФЭМЯѓЙ§Еу(Ѓ1,0)КЭЕу(3,0)ЃЌгаЯТСаЫЕЗЈЃКЂйbcЃМ0ЃЛЂкaЃЋbЃЋcЃО0ЃЛЂл2aЃЋbЃН0ЃЛЂм4acЃОb2ЃЎЦфжаДэЮѓЕФЪЧ(ЁЁЁЁ)
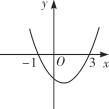
A.ЂкЂмB.ЂйЂлЂмC.ЂйЂкЂмD.ЂкЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊжБЯп![]() гы
гы![]() жсКЭ
жсКЭ![]() жсЗжБ№НЛгкЕу
жсЗжБ№НЛгкЕу![]() КЭЕу
КЭЕу![]() ХзЮяЯп
ХзЮяЯп![]() ОЙ§Еу
ОЙ§Еу![]() гыжБЯп
гыжБЯп![]() ЕФСэвЛИіНЛЕуЮЊ
ЕФСэвЛИіНЛЕуЮЊ![]() ЃЎ
ЃЎ
![]() Чѓ
Чѓ![]() ЕФжЕКЭХзЮяЯпЕФНтЮіЪН
ЕФжЕКЭХзЮяЯпЕФНтЮіЪН
![]() Еу
Еу![]() дкХзЮяЯпЩЯЃЌ
дкХзЮяЯпЩЯЃЌ![]() жсНЛжБЯп
жсНЛжБЯп![]() гкЕу
гкЕу![]() Еу
Еу![]() дкжБЯп
дкжБЯп![]() ЩЯЃЌЧвЫФБпаЮ
ЩЯЃЌЧвЫФБпаЮ![]() ЮЊОиаЮЃЎЩшЕу
ЮЊОиаЮЃЎЩшЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]() ОиаЮ
ОиаЮ![]() ЕФжмГЄЮЊ
ЕФжмГЄЮЊ![]() Чѓ
Чѓ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНвдМА
ЕФКЏЪ§ЙиЯЕЪНвдМА![]() ЕФзюДѓжЕ
ЕФзюДѓжЕ
![]() НЋ
НЋ![]() ШЦЦНУцФкФГЕу
ШЦЦНУцФкФГЕу![]() ФцЪБеыа§зЊ
ФцЪБеыа§зЊ![]() ЕУЕН
ЕУЕН![]() ЃЈЕу
ЃЈЕу![]() ЗжБ№гы
ЗжБ№гы![]() ЕуЖдгІ)ЃЌШє
ЕуЖдгІ)ЃЌШє![]() ЕФСНИіЖЅЕуЧЁКУТфдкХзЮяЯпЩЯЃЌЧыжБНгаДГіЕу
ЕФСНИіЖЅЕуЧЁКУТфдкХзЮяЯпЩЯЃЌЧыжБНгаДГіЕу![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
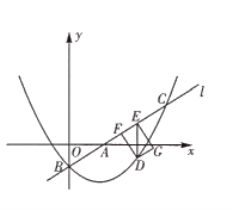
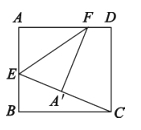
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮ ABCD жаЃЌEЪЧBCЕФжаЕуЃЌFЪЧCDЩЯвЛЕуЃЌAEЁЭEFЃЎгаЯТСаНсТлЃК
ЂйЁЯBAEЃН30ЁуЃЛ
ЂкЩфЯпFEЪЧЁЯAFCЕФНЧЦНЗжЯпЃЛ
ЂлCFЃН![]() CDЃЛ
CDЃЛ
ЂмAFЃНABЃЋCFЃЎ
Цфжае§ШЗНсТлЕФИіЪ§ЮЊЃЈ ЃЉ
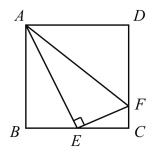
A.1 ИіB.2 ИіC.3 ИіD.4 Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌФГНЈжўЮяЕФЖЅВПгавЛПщБъЪЖХЦ CDЃЌаЁУїдкаБЦТЩЯ B ДІВтЕУБъЪЖХЦЖЅВПC ЕФбіНЧЮЊ 45ЁуЃЌ биаБЦТзпЯТРДдкЕиУц A ДІВтЕУБъЪЖХЦЕзВП D ЕФбіНЧЮЊ 60ЁуЃЌвбжЊаБЦТ AB ЕФЦТНЧЮЊ 30ЁуЃЌABЃНAEЃН10 УзЃЎдђБъЪЖХЦ CD ЕФИпЖШЪЧ( )УзЃЎ
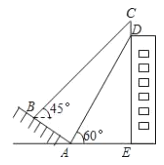
A.15Ѓ5![]() B.20Ѓ10
B.20Ѓ10![]() C.10Ѓ5
C.10Ѓ5![]() D.5
D.5![]() Ѓ5
Ѓ5
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌФГНЈжўЮяЕФЖЅВПгавЛПщБъЪЖХЦ CDЃЌаЁУїдкаБЦТЩЯ B ДІВтЕУБъЪЖХЦЖЅВПC ЕФбіНЧЮЊ 45ЁуЃЌ биаБЦТзпЯТРДдкЕиУц A ДІВтЕУБъЪЖХЦЕзВП D ЕФбіНЧЮЊ 60ЁуЃЌвбжЊаБЦТ AB ЕФЦТНЧЮЊ 30ЁуЃЌABЃНAEЃН10 УзЃЎдђБъЪЖХЦ CD ЕФИпЖШЪЧ( )УзЃЎ
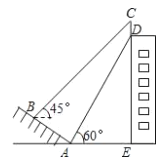
A.15Ѓ5![]() B.20Ѓ10
B.20Ѓ10![]() C.10Ѓ5
C.10Ѓ5![]() D.5
D.5![]() Ѓ5
Ѓ5
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁїABCКЭЁїCDEЖМЪЧЕШбќШ§НЧаЮЃЌЁЯBACЃНЁЯEDCЃН120ЁуЃЎ
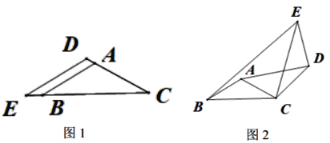
ЃЈ1ЃЉШчЭМ1ЃЌAЁЂDЁЂCдкЭЌвЛжБЯпЩЯЪБЃЌ![]() ЃН_______ЃЌ
ЃН_______ЃЌ![]() ЃН_______ЃЛ
ЃН_______ЃЛ
ЃЈ2ЃЉдкЭМ1ЕФЛљДЁЩЯЃЌЙЬЖЈЁїABCЃЌНЋЁїCDEШЦCа§зЊвЛЖЈЕФНЧЖШІС(0ЁуЃМІСЃМ360Ёу)ЃЌШчЭМ2ЃЌСЌНгADЁЂBEЃЎ
Ђй ![]() ЕФжЕгаУЛгаИФБфЃПЧыЫЕУїРэгЩЃЎ
ЕФжЕгаУЛгаИФБфЃПЧыЫЕУїРэгЩЃЎ
ЂкЭиеЙбаОПЃКШєABЃН1ЃЌDEЃН![]() ЃЌЕБ BЁЂDЁЂEдкЭЌвЛжБЯпЩЯЪБЃЌЧыМЦЫуЯпЖЮADЕФГЄЃЛ
ЃЌЕБ BЁЂDЁЂEдкЭЌвЛжБЯпЩЯЪБЃЌЧыМЦЫуЯпЖЮADЕФГЄЃЛ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
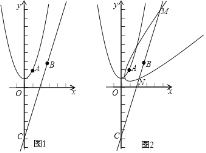
ЁОЬтФПЁПШчЭМ1ЃЌвбжЊХзЮяЯпЕФЖЅЕузјБъЮЊЃЈ0ЃЌ1ЃЉЧвОЙ§ЕуAЃЈ1ЃЌ2ЃЉЃЌжБЯпyЃН3xЉ4![]() ОЙ§ЕуBЃЈ
ОЙ§ЕуBЃЈ![]() ЃЌnЃЉЃЌгыyжсНЛЕуЮЊCЃЎ
ЃЌnЃЉЃЌгыyжсНЛЕуЮЊCЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНМАnЕФжЕЃЛ
ЃЈ2ЃЉНЋжБЯпBCШЦдЕуOФцЪБеыа§зЊ45ЁуЃЌЧѓа§зЊКѓЕФжБЯпЕФНтЮіЪНЃЛ
ЃЈ3ЃЉШчЭМ2НЋХзЮяЯпШЦдЕуOЫГЪБеыа§зЊ45ЁуЕУЕНаТЧњЯпЃЌаТЧњЯпгыжБЯпBCНЛгкЕуMЁЂNЃЌЕуMдкЕуNЕФЩЯЗНЃЌЧѓЕуNЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮ![]() жаЃЌ
жаЃЌ![]() ЗжБ№ЪЧБп
ЗжБ№ЪЧБп![]() ЩЯЕФЕуЃЌ
ЩЯЕФЕуЃЌ![]() ЃЌНЋ
ЃЌНЋ![]() би
би![]() ЫљдкжБЯпелЕўЃЌЕу
ЫљдкжБЯпелЕўЃЌЕу![]() ЕФЖдгІЕу
ЕФЖдгІЕу![]() е§КУТфдкЯпЖЮ
е§КУТфдкЯпЖЮ![]() ЩЯЃЌШє
ЩЯЃЌШє![]() ЃЌдђелКл
ЃЌдђелКл![]() ЕФГЄЮЊ__________ЃЎ
ЕФГЄЮЊ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com