
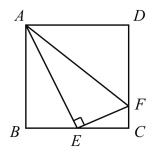
【题目】如图,在正方形 ABCD 中,E是BC的中点,F是CD上一点,AE⊥EF.有下列结论:
①∠BAE=30°;
②射线FE是∠AFC的角平分线;
③CF=![]() CD;
CD;
④AF=AB+CF.
其中正确结论的个数为( )
A.1 个B.2 个C.3 个D.4 个
【答案】B
【解析】
根据点E为BC中点和正方形的性质,得出∠BAE的正切值,从而判断①,再证明△ABE∽△ECF,利用有两边对应成比例且夹角相等三角形相似即可证得△ABE∽△AEF,可判断②③,过点E作AF的垂线于点G,再证明△ABE≌△AGE,△ECF≌△EGF,即可证明④.
解:∵E是BC的中点,
∴tan∠BAE=![]() ,
,
∴∠BAE![]() 30°,故①错误;
30°,故①错误;
∵四边形ABCD是正方形,
∴∠B=∠C=90°,AB=BC=CD,
∵AE⊥EF,
∴∠AEF=∠B=90°,
∴∠BAE+∠AEB=90°,∠AEB+FEC=90°,
∴∠BAE=∠CEF,
在△BAE和△CEF中,
![]() ,
,
∴△BAE∽△CEF,
∴![]() ,
,
∴BE=CE=2CF,
∵BE=CF=![]() BC=
BC=![]() CD,
CD,
即2CF=![]() CD,
CD,
∴CF=![]() CD,
CD,
故③错误;
设CF=a,则BE=CE=2a,AB=CD=AD=4a,DF=3a,
∴AE=![]() a,EF=
a,EF=![]() a,AF=5a,
a,AF=5a,
∴![]() ,
,![]() ,
,
∴![]() ,
,
又∵∠B=∠AEF,
∴△ABE∽△AEF,
∴∠AEB=∠AFE,∠BAE=∠EAG,
又∵∠AEB=∠EFC,
∴∠AFE=∠EFC,
∴射线FE是∠AFC的角平分线,故②正确;
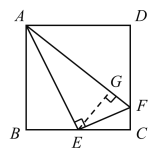
过点E作AF的垂线于点G,
在△ABE和△AGE中,
 ,
,
∴△ABE≌△AGE(AAS),
∴AG=AB,GE=BE=CE,
在Rt△EFG和Rt△EFC中,
![]() ,
,
Rt△EFG≌Rt△EFC(HL),
∴GF=CF,
∴AB+CF=AG+GF=AF,故④正确.
故选B.


科目:初中数学 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗. 我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整). 请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;

查看答案和解析>>
科目:初中数学 来源: 题型:
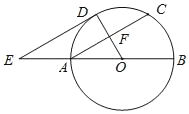
【题目】如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交弧AC于点D,过点D作⊙O的切线,交BA的延长线于点E.
(1)求证:AC∥DE;
(2)连接AD、CD、OC.填空
①当∠OAC的度数为 时,四边形AOCD为菱形;
②当OA=AE=2时,四边形ACDE的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某店代理某品牌商品的销售.已知该品牌商品进价每件40元,日销售y(件)与销售价x(元/件)之间的关系如图所示(实线),付员工的工资每人每天100元,每天还应支付其它费用150元.
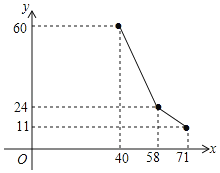
(1)求日销售y(件)与销售价x(元/件)之间的函数关系式;
(2)该店员工人共3人,若某天收支恰好平衡(收入=支出),求当天的销售价是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解学生对“预防新型冠状病毒”知识的掌握情况,学校组织了一次线上知识培训,培训结束后进行测试,在全校2000名学生中,分别抽取了男生,女生各15份成绩,整理分析过程如下,请补充完整.
(收集数据)
15名男生测试成绩统计如下:(满分100分)78,90,99,93,92,95,94,100,90,85,86,95,75,88,90
15名女生测试成绩统计如下:(满分100分)77,82,83,86,90,90,92,91,93,92,92,92,92,98,100
(整理、描述数据)
70.5~75.5 | 75.5~80.5 | 80.5~85.5 | 85.5~90.5 | 90.5~95.5 | 95.5~100.5 | |
男生 | 1 | 1 | 1 | 5 | 5 | 2 |
女生 | 0 | 1 | 2 | 3 | 7 | 2 |
(分析数据)
(1)两组样本数据的平均数、众数、中位数、方差如下表所示:
性别 | 平均数 | 众数 | 中位数 | 方差 |
男生 | 90 | 90 | 90 | 44.9 |
女生 | 90 |
|
| 32.8 |
在表中:![]() ________.
________.![]() ________;
________;
(2)若规定得分在80分以上(不含80分)为合格,请估计全校学生中“预防新型冠状病毒”知识测试合格的学生有多少人?
(3)通过数据分析得到的结论,你认为男生和女生中谁的成绩比较好?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,且点
,且点![]() 与点
与点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,点
,点![]() 是抛物线的顶点.
是抛物线的顶点.

(1)求二次函数的关系式.
(2)点![]() 为线段
为线段![]() 上一个动点,过点
上一个动点,过点![]() 作
作![]() 轴于点
轴于点![]() .若
.若![]() ,
,![]() 的面积为
的面积为![]() .
.
①求![]() 与
与![]() 的函数关系式,写出自变量
的函数关系式,写出自变量![]() 的取值范围.
的取值范围.
②当![]() 取得最值时,求点
取得最值时,求点![]() 的坐标.
的坐标.
(3)在![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为直角三角形?如果存在,请直接写出点
为直角三角形?如果存在,请直接写出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划组织学生参加“书法”、“摄影”、“航模”、“围棋”四个课外兴趣小组,要求每人必须参加,并且只能选择其中一个小组,为了解学生对四个课外兴趣小组的选择情况,学校从全体学生中随机抽取部分学生进行问卷调查,并把调查结果制成如图所示的扇形统计图和条形统计图(部分信息未给出),请你根据给出的信息解答下列问题:

(1)求参加这次问卷调查的学生人数,并补全条形统计图(画图后请标注相应的数据);
(2)m=_______,n=_______;
(3)若该校共有1200名学生,试估计该校选择“围棋”课外兴趣小组的学生有多少人?
(4)分别用A、B、C、D表示“书法”、“摄影”、“航模”、“围棋”,小明和小红从中各选取一个小组,请用树状图法或列表法求出“两人选择小组不同”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家计划2035年前实施新能源汽车,某公司为加快新旧动能转换,提高公司经济效益,决定对近期研发出的一种新型能源产品进行降价促销.根据市场调查:这种新型能源产品销售单价定为200元时,每天可售出300个;若销售单价每降低1元,每天可多售出5个.已知每个新型能源产品的成本为100元.
问:(1)设该产品的销售单价为![]() 元,每天的利润为
元,每天的利润为![]() 元.则
元.则![]() _________(用含
_________(用含![]() 的代数式表示)
的代数式表示)
(2)这种新型能源产品降价后的销售单价为多少元时,公司每天可获利32000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司开发处一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为10元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘制成图象,图中的折线ABC表示日销售量y(件)与销售时间x(天)之间的函数关系.

(1)求y与x之间的函数表达式,并写出x的取值范围;
(2)若该节能产品的日销售利润为W(元),求W与x之间的函数表达式,并求出日销售利润不超过1040元的天数共有多少天?
(3)若5≤x≤17,直接写出第几天的日销售利润最大,最大日销售利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com