
【题目】如图,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,且点
,且点![]() 与点
与点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,点
,点![]() 是抛物线的顶点.
是抛物线的顶点.

(1)求二次函数的关系式.
(2)点![]() 为线段
为线段![]() 上一个动点,过点
上一个动点,过点![]() 作
作![]() 轴于点
轴于点![]() .若
.若![]() ,
,![]() 的面积为
的面积为![]() .
.
①求![]() 与
与![]() 的函数关系式,写出自变量
的函数关系式,写出自变量![]() 的取值范围.
的取值范围.
②当![]() 取得最值时,求点
取得最值时,求点![]() 的坐标.
的坐标.
(3)在![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为直角三角形?如果存在,请直接写出点
为直角三角形?如果存在,请直接写出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
【答案】(1)![]() ;(2)①
;(2)①![]() ,
,![]() ;②P(
;②P(![]() ,3);
,3);
(3)![]() 或
或![]()
【解析】
(1)将点B、C的坐标代入![]() 即可;
即可;
(2)①求出顶点坐标,直线MB的解析式等,由PD⊥x轴且OD=m知P(m,-2m+6),即可用含m的代数式表示出S;
②在和①的情况下,将S和m的关系式化为顶点式,由二次函数的图象和性质即可写出点P的坐标;
(3)分情况讨论,当∠CPD=90°时,推出PD=CO=3,则点P的纵坐标为3,即可求出点P的坐标;当∠PCD=90°时,证∠PDC=∠OCD,由锐角三角函数可求出m的值,即可写出点P的坐标;当∠PDC=90°时,不存在点P.
解:(1)将![]() ,
,![]() 代入
代入![]() ,
,
得![]() ,
,
解得![]() ,
,
∴二次函数的解析式为![]() ;
;
(2)①∵![]()
∴顶点M(1,4),
将直线BM的解析式设为![]() ,
,
将点![]() ,M(1,4)代入,
,M(1,4)代入,
可得![]() ,
,
解得![]() ,
,
∴直线BM的解析式为![]() ,
,
如图∵PD⊥x轴且OD=m,
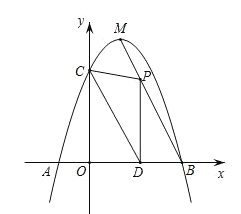
∴P(m,-2m+6),
∴![]() ,
,
即![]() ,
,
∵点![]() 为线段
为线段![]() 上一个动点且
上一个动点且![]() ,M(1,4),
,M(1,4),
∴![]() ;
;
②![]() ,
,
∴当![]() 时,S取最大值
时,S取最大值![]() ,
,
∴P(![]() ,3);
,3);
(3)存在,理由如下:
如图,当∠CPD=90°时,
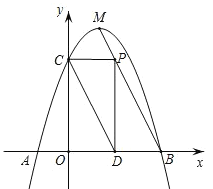
![]() ,
,
∴四边形CODP为矩形,
∵PD=CO=3,
将![]() 代入直线
代入直线![]() ,
,
得![]() ,
,
∴P![]() ;
;
如图,当∠PCD=90°时,

∵OC=3,OD=m,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
解得![]() (舍去),
(舍去),![]() ,
,
∴![]() ;
;
当∠PDC=90°时,
∵PD⊥x轴,
∴不存在点P;
综上所述,点P的坐标为![]() 或
或![]() .
.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】垃圾的分类处理与回收利用,可以减少污染,节省资源.某城市环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,其相关信息如下:

根据图表解答下列问题:
(1)请将条形统计图补充完整;
(2)在扇形统计图样中,产生的有害垃圾C所对应的圆心角 度;
(3)调查发现,在可回收物中塑料类垃圾占13%,每回收1吨塑料类垃圾可获得0.5吨二级原料.假设该城市每月产生的生活垃圾为1000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
查看答案和解析>>
科目:初中数学 来源: 题型:
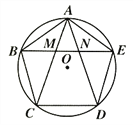
【题目】如图,正五边形的边长为2,连接对角线AD、BE、CE,线段AD分别与BE和CE相交于点M、N,给出下列结论:①∠AME=108°,②AN2=AMAD;③MN=3-![]() ;④S△EBC=2
;④S△EBC=2![]() -1,其中正确的结论是_________(把你认为正确结论的序号都填上).
-1,其中正确的结论是_________(把你认为正确结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
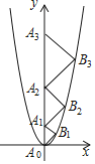
【题目】二次函数![]() 的图象如图,点
的图象如图,点![]() 位于坐标原点,点
位于坐标原点,点![]() ,
,![]() ,
,![]() ,…,
,…,![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() ,
,![]() ,
,![]() ,…,
,…,![]() 在二次函数
在二次函数![]() 位于第一象限的图象上,
位于第一象限的图象上,![]() ,
,![]() ,
,![]() ,…,
,…,![]() 都是直角顶点在抛物线上的等腰直角三角形,则
都是直角顶点在抛物线上的等腰直角三角形,则![]() 的斜边长为________.
的斜边长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形 ABCD 中,E是BC的中点,F是CD上一点,AE⊥EF.有下列结论:
①∠BAE=30°;
②射线FE是∠AFC的角平分线;
③CF=![]() CD;
CD;
④AF=AB+CF.
其中正确结论的个数为( )
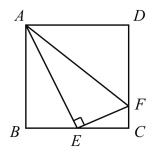
A.1 个B.2 个C.3 个D.4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人加工同一种零件,甲每天加工的数量是乙每天加工数量的1.5倍,两人各加工300个这种零件,甲比乙少用5天.
(1)求甲、乙两人每天各加工多少个这种零件?
(2)已知甲、乙两人加工这种零件每天的加工费分别是150元和120元,现有1500个这种零件的加工任务,甲单独加工一段时间后另有安排,剩余任务由乙单独完成.如果总加工费为7800元,那么甲、乙各加工了多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某建筑物的顶部有一块标识牌 CD,小明在斜坡上 B 处测得标识牌顶部C 的仰角为 45°, 沿斜坡走下来在地面 A 处测得标识牌底部 D 的仰角为 60°,已知斜坡 AB 的坡角为 30°,AB=AE=10 米.则标识牌 CD 的高度是( )米.
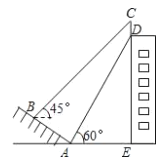
A.15-5![]() B.20-10
B.20-10![]() C.10-5
C.10-5![]() D.5
D.5![]() -5
-5
查看答案和解析>>
科目:初中数学 来源: 题型:
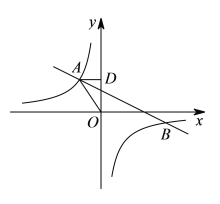
【题目】如图,在平面直角坐标系中,反比例函数![]()
![]() 与一次函数
与一次函数![]() 交于第二、四象限的
交于第二、四象限的![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() ,
,![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求反比例函数和一次函数的解析式;
(2)请根据图象直接写出![]() 的自变量
的自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com