
【题目】二次函数![]() 的图象如图,点
的图象如图,点![]() 位于坐标原点,点
位于坐标原点,点![]() ,
,![]() ,
,![]() ,…,
,…,![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() ,
,![]() ,
,![]() ,…,
,…,![]() 在二次函数
在二次函数![]() 位于第一象限的图象上,
位于第一象限的图象上,![]() ,
,![]() ,
,![]() ,…,
,…,![]() 都是直角顶点在抛物线上的等腰直角三角形,则
都是直角顶点在抛物线上的等腰直角三角形,则![]() 的斜边长为________.
的斜边长为________.
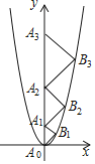
【答案】4040
【解析】
如图所示,过点B1,B2,B3分别作y轴的垂线,垂足分别为C,D,E,分别写出直线A0B1、直线A1B2、直线A2B3的解析式,将它们分别与y=x2联立,求得点B1,B2,B3的坐标,从而可得A0A1=2,A1A2=4,A2A3=6,发现规律后,按照规律即可求得![]() 的斜边长.
的斜边长.
解:如图所示,过点B1,B2,B3分别作y轴的垂线,垂足分别为C,D,E
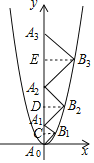
∵△A0B1A1,△A1B2A2,△A2B3A3…△A9B10A10都是直角顶点在抛物线上的等腰直角三角形
∴∠B1A0A1=∠B2A1A2=∠B3A2A3=45°
∴A0B1所在直线的解析式为:y=x
由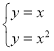 ,得B1(1,1)
,得B1(1,1)
∴A0A1=2B1C=2
∴A1(0,2)
∴直线A1B2为:y=x+2
由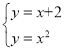 ,得B2(2,4)
,得B2(2,4)
∴A1A2=2B2D=4
∴A2(0,6)
∴直线A2B3为:y=x+6
由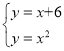 ,得B3(3,9)
,得B3(3,9)
∴A2A3=2B3E=6
…
由上面A0A1=2,A1A2=4,A2A3=6,可以看出这些直角顶点在抛物线上的等腰直角三角形的斜边长依次加2
∴![]() 的斜边长为2+2019×2=4040
的斜边长为2+2019×2=4040
故答案为:4040.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉,进市场调查,甲种花卉的种植费用y(元)与种植面积xm2之间的函数关系如图所示,乙种花卉的种植费用为100元/m2.
(1)请直接写出当0≤x≤300和x>300时,y与x的函数关系式;

(2)广场上甲、乙两种花卉的种植面积共1200m2,如果甲种花卉的种植面积不少于200m2,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植总费用最少?最少总费用为多少元?
(3)在(2)的条件下,若种植总费用不小于123000元,求出甲种花卉种植面积的范围是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 内接于
内接于![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() ,交
,交![]() 边于点
边于点![]() ,且
,且![]() .
.
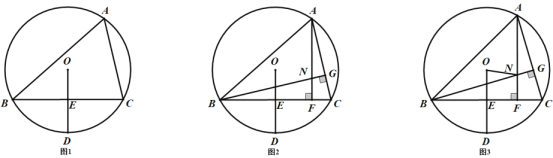
(1)如图1,求![]() 的度数;
的度数;
(2)如图2,作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 交于点
交于点![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,连接![]() ,若
,若![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在同一直角坐标系xOy中,有双曲线![]() ,直线y2=k2x+b1,y3=k3x+b2,且点A(2,5),点B(﹣6,n)在双曲线的图象上
,直线y2=k2x+b1,y3=k3x+b2,且点A(2,5),点B(﹣6,n)在双曲线的图象上
(1)求y1和y2的解析式;
(2)若y3与直线x=4交于双曲线,且y3∥y2,求y3的解析式;
(3)直接写出![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某店代理某品牌商品的销售.已知该品牌商品进价每件40元,日销售y(件)与销售价x(元/件)之间的关系如图所示(实线),付员工的工资每人每天100元,每天还应支付其它费用150元.
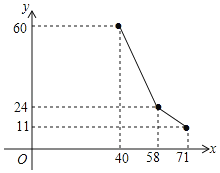
(1)求日销售y(件)与销售价x(元/件)之间的函数关系式;
(2)该店员工人共3人,若某天收支恰好平衡(收入=支出),求当天的销售价是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]()
![]() 经过
经过![]() ,
,![]() 两点,点
两点,点![]() 为抛物线的顶点,抛物线的对称轴与
为抛物线的顶点,抛物线的对称轴与![]() 轴交于点
轴交于点![]() .
.

(1)求抛物线的解析式;
(2)动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 向终点
向终点![]() 作匀速运动,速度为每秒1个单位长度,运动时间为
作匀速运动,速度为每秒1个单位长度,运动时间为![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,以
,以![]() 为正方形的一边,向上作正方形
为正方形的一边,向上作正方形![]() ,边
,边![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .
.
①当![]() 为何值时,点
为何值时,点![]() 落在抛物线上;
落在抛物线上;
②在点![]() 运动过程中,是否存在某一时刻,使得四边形
运动过程中,是否存在某一时刻,使得四边形![]() 为平行四边形?若存在,求出此时刻的
为平行四边形?若存在,求出此时刻的![]() 值;若不存在,请说明理由.
值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,且点
,且点![]() 与点
与点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,点
,点![]() 是抛物线的顶点.
是抛物线的顶点.

(1)求二次函数的关系式.
(2)点![]() 为线段
为线段![]() 上一个动点,过点
上一个动点,过点![]() 作
作![]() 轴于点
轴于点![]() .若
.若![]() ,
,![]() 的面积为
的面积为![]() .
.
①求![]() 与
与![]() 的函数关系式,写出自变量
的函数关系式,写出自变量![]() 的取值范围.
的取值范围.
②当![]() 取得最值时,求点
取得最值时,求点![]() 的坐标.
的坐标.
(3)在![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为直角三角形?如果存在,请直接写出点
为直角三角形?如果存在,请直接写出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划组织学生参加“书法”、“摄影”、“航模”、“围棋”四个课外兴趣小组,要求每人必须参加,并且只能选择其中一个小组,为了解学生对四个课外兴趣小组的选择情况,学校从全体学生中随机抽取部分学生进行问卷调查,并把调查结果制成如图所示的扇形统计图和条形统计图(部分信息未给出),请你根据给出的信息解答下列问题:

(1)求参加这次问卷调查的学生人数,并补全条形统计图(画图后请标注相应的数据);
(2)m=_______,n=_______;
(3)若该校共有1200名学生,试估计该校选择“围棋”课外兴趣小组的学生有多少人?
(4)分别用A、B、C、D表示“书法”、“摄影”、“航模”、“围棋”,小明和小红从中各选取一个小组,请用树状图法或列表法求出“两人选择小组不同”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过B(3,0),C(0,-3)两点,点D为顶点.
经过B(3,0),C(0,-3)两点,点D为顶点.
(1)求抛物线的解析式及顶点D的坐标;
(2)点E在抛物线的对称轴上,F在BD上,求BE+EF的最小值;
(3)点P是抛物线第四象限的点(不与B、C重合),连接PB,以PB为边作正方形BPMN,当点M或N恰好落在对称轴上时,求出对应的P点的坐标(结果保留根号).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com