
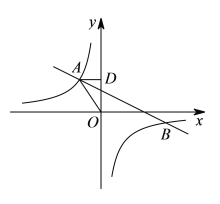
【题目】如图,在平面直角坐标系中,反比例函数![]()
![]() 与一次函数
与一次函数![]() 交于第二、四象限的
交于第二、四象限的![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() ,
,![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求反比例函数和一次函数的解析式;
(2)请根据图象直接写出![]() 的自变量
的自变量![]() 的取值范围.
的取值范围.
【答案】(1) 反比例函数的解析式为y=﹣![]() ,一次函数的解析式为y=﹣
,一次函数的解析式为y=﹣![]() x+2.(2)x≤﹣2或0<x≤6.
x+2.(2)x≤﹣2或0<x≤6.
【解析】
(1)根据S△AOD=3可得AD=2,根据反比例函数的特点k=xy为定值,列出方程,求出k的值,便可求出反比例函数的解析式;根据k的值求出B点的坐标,用待定系数法便可求出一次函数的解析式.
(2)根据函数图象可直接解答.
(1)∵AD⊥y轴于点D,OD=3,
∴![]() ,
,
∴AD=2.即A(﹣2,3),
将A点坐标代入y=![]() (k≠0),得k=﹣2×3=﹣6.
(k≠0),得k=﹣2×3=﹣6.
反比例函数的解析式为y=﹣![]() .
.
将B点坐标代入y=﹣![]() 中,得﹣1=﹣
中,得﹣1=﹣![]() ,解得n=6.即B(6,﹣1),
,解得n=6.即B(6,﹣1),
将A、B两点坐标代入y=ax+b,得![]() ,解得
,解得 .
.
所以一次函数的解析式为y=﹣![]() x+2.
x+2.
(2)ax+b≥![]() 的自变量x的取值范围是x≤﹣2或0<x≤6.
的自变量x的取值范围是x≤﹣2或0<x≤6.


科目:初中数学 来源: 题型:
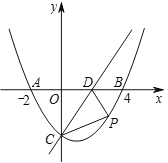
【题目】如图,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,且点
,且点![]() 与点
与点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,点
,点![]() 是抛物线的顶点.
是抛物线的顶点.

(1)求二次函数的关系式.
(2)点![]() 为线段
为线段![]() 上一个动点,过点
上一个动点,过点![]() 作
作![]() 轴于点
轴于点![]() .若
.若![]() ,
,![]() 的面积为
的面积为![]() .
.
①求![]() 与
与![]() 的函数关系式,写出自变量
的函数关系式,写出自变量![]() 的取值范围.
的取值范围.
②当![]() 取得最值时,求点
取得最值时,求点![]() 的坐标.
的坐标.
(3)在![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为直角三角形?如果存在,请直接写出点
为直角三角形?如果存在,请直接写出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办园博会知识竞赛,打算购买A、B两种奖品.如果购买A奖品10件、B奖品5件,共需120元;如果购买A奖品5件、B奖品10件,共需90元.
(1)A,B两种奖品每件各多少元?
(2)若购买A、B奖品共100件,总费用不超过600元,则A奖品最多购买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过B(3,0),C(0,-3)两点,点D为顶点.
经过B(3,0),C(0,-3)两点,点D为顶点.
(1)求抛物线的解析式及顶点D的坐标;
(2)点E在抛物线的对称轴上,F在BD上,求BE+EF的最小值;
(3)点P是抛物线第四象限的点(不与B、C重合),连接PB,以PB为边作正方形BPMN,当点M或N恰好落在对称轴上时,求出对应的P点的坐标(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司开发处一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为10元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘制成图象,图中的折线ABC表示日销售量y(件)与销售时间x(天)之间的函数关系.

(1)求y与x之间的函数表达式,并写出x的取值范围;
(2)若该节能产品的日销售利润为W(元),求W与x之间的函数表达式,并求出日销售利润不超过1040元的天数共有多少天?
(3)若5≤x≤17,直接写出第几天的日销售利润最大,最大日销售利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,与直线
,与直线![]() 交于点
交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求该抛物线的解析式.
(2)点![]() 是抛物线上第四象限上的一个动点,连接
是抛物线上第四象限上的一个动点,连接![]() ,
,![]() ,当
,当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标.
的坐标.
(3)将抛物线的对称轴向左平移3个长度单位得到直线![]() ,点
,点![]() 是直线
是直线![]() 上一点,连接
上一点,连接![]() ,
,![]() ,若直线
,若直线![]() 上存在使
上存在使![]() 最大的点
最大的点![]() ,请直接写出满足条件的点
,请直接写出满足条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
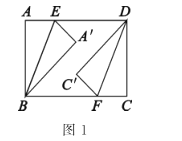
动手操作:如图1,四边形![]() 是一张矩形纸片,
是一张矩形纸片,![]() ,点
,点![]() 分别在
分别在![]() 边上,且
边上,且![]() ,连接
,连接![]() ,将
,将![]() 分别沿
分别沿![]() 折叠,点
折叠,点![]() 分别落在点
分别落在点![]() 处.
处.
探究展示:(1)“刻苦小组”发现:![]() ,且
,且![]() ,并展示了如下的证明过程.
,并展示了如下的证明过程.
证明:在矩形![]() 中,
中,![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() (依据1)
(依据1)
∴![]() ,
,
∴![]() (依据2)
(依据2)
反思交流:①上述证明过程中的“依据1”与“依据2”分别指什么?
②“勤奋小组”认为:还可以通过证明四边形![]() 是平行四边形获证,请你根据“勤奋小组”的证明思路写出证明过程.
是平行四边形获证,请你根据“勤奋小组”的证明思路写出证明过程.
猜想证明:(2)如图2,折叠过程中,当点![]() 在直线
在直线![]() 的同侧时,延长
的同侧时,延长![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() 中,则四边形
中,则四边形![]() 是什么特殊四边形?请说明理由.
是什么特殊四边形?请说明理由.
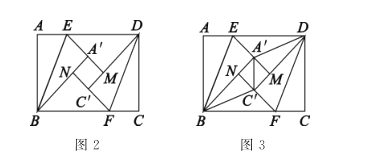
联想拓广:(3)如图3,连接![]() ,
,
①当![]() 时,
时,![]() 的长为_____________________;
的长为_____________________;
②![]() 的长有最小值吗?若有,请你直接写出
的长有最小值吗?若有,请你直接写出![]() 的最小值;若没有,请说明理由.
的最小值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳某百果园店售卖赣南脐橙,已知每千克脐橙的成本价为![]() 元,在销售脐橙的这
元,在销售脐橙的这![]() 天时间内,销售单价
天时间内,销售单价![]() (元/千克)与时间第
(元/千克)与时间第![]() (天)之间的函数关系式为
(天)之间的函数关系式为![]() (
(![]() ,且
,且![]() 为整数),日销售量
为整数),日销售量![]() (千克)与时间第
(千克)与时间第![]() (天)之间的函数关系式为
(天)之间的函数关系式为![]() (
(![]() ,且
,且![]() 为整数)
为整数)
(1)请你直接写出日销售利润![]() (元)与时间第
(元)与时间第![]() (天)之间的函数关系式;
(天)之间的函数关系式;
(2)该店有多少天日销售利润不低于![]() 元?
元?
(3)在实际销售中,该店决定每销售![]() 千克脐橙,就捐赠
千克脐橙,就捐赠![]() 元给希望工程,在这
元给希望工程,在这![]() 天中,每天扣除捐赠后的日销售利润随时间
天中,每天扣除捐赠后的日销售利润随时间![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,弦
的直径,弦![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() .
.
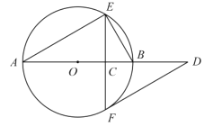
(1)已知![]() ,求
,求![]() 的大小(用含
的大小(用含![]() 的式子表示);
的式子表示);
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,请补全图形;若
,请补全图形;若![]() ,
,![]() ,求
,求![]() 的半径.
的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com